题目内容
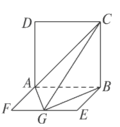
如图,平面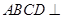 平面
平面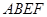 ,四边形
,四边形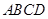 是正方形,四边形
是正方形,四边形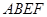 是矩形,且
是矩形,且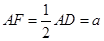 ,
,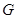 是
是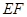 的中点,则
的中点,则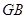 与平面
与平面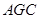 所成角的正弦值为( )
所成角的正弦值为( )
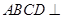 平面
平面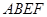 ,四边形
,四边形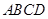 是正方形,四边形
是正方形,四边形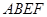 是矩形,且
是矩形,且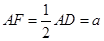 ,
, 是
是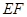 的中点,则
的中点,则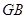 与平面
与平面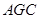 所成角的正弦值为( )
所成角的正弦值为( )
A.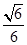 | B.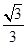 | C.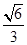 | D.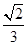 |
C
试题分析:由已知可知图中直线
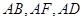 两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出
两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出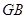 与平面
与平面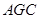 所成角的正弦值.
所成角的正弦值.
练习册系列答案
相关题目
题目内容
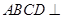 平面
平面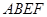 ,四边形
,四边形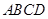 是正方形,四边形
是正方形,四边形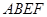 是矩形,且
是矩形,且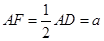 ,
, 是
是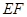 的中点,则
的中点,则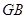 与平面
与平面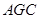 所成角的正弦值为( )
所成角的正弦值为( )
A.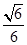 | B.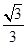 | C.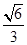 | D.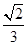 |
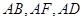 两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出
两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出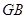 与平面
与平面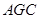 所成角的正弦值.
所成角的正弦值.