题目内容
4.已知命题P:存在x∈R,x3=1-x2;命题q:△ABC中,“A>B”是“sinA>sinB”的充分条件;则下列命题是真命题的是( )| A. | p且q | B. | p或?q | C. | ?p且?q | D. | ?p或q |
分析 分别判断出p,q的真假,从而判断出复合命题的真假.
解答 解:关于命题P:存在x∈R,x3=1-x2;画出函数y=x3和y=1-x2的图象,如图示: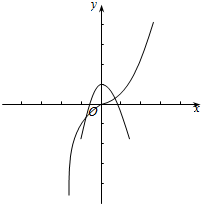 ,
,
故命题p是真命题;
命题q:在△ABC中“sinA>sinB”?2cos $\frac{A+B}{2}$sin $\frac{A-B}{2}$>0?“A>B”,
因此,“A>B”是“sinA>sinB”的充要条件,
∴q是真命题.
故选:A.
点评 本题考查了复合命题的判断,考查函数问题,是一道基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.动直线x=m(m>0)与函数f(x)=2x+$\frac{1}{x}$,g(x)=x-$\frac{1}{x}$-lnx分别交于点A,B,则|AB|的最小值为( )
| A. | 3+ln2 | B. | 2 | C. | $\frac{7}{2}$-ln2 | D. | 3 |
15.(文)设全集U=R,集合A={x|x2+4x<0},集合B={x|x<-2},则图中阴影部分表示的集合为( )
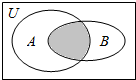

| A. | {x|-4<x<-2} | B. | {x|-4<x<0} | C. | {x|x>0} | D. | {x|x<-2} |
9.已知集合A={-2,-1,0,1,2},B={x|x2-3x-4<0},则A∩B=( )
| A. | (-1,1) | B. | {-1,0,1} | C. | (0,2) | D. | {0,1,2} |