题目内容
已知函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对任意的x1,x2∈[0,1]
且x1≠x2,都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<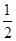 ,若用反证法证明该题,则反设应为________.
,若用反证法证明该题,则反设应为________.
且x1≠x2,都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<
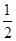 ,若用反证法证明该题,则反设应为________.
,若用反证法证明该题,则反设应为________.存在x1,x2∈[0,1]且x1≠x2,虽然|f(x1)-f(x2)|<|x1-x2|,但|f(x1)-f(x2)|≥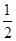
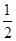
根据已知和反证法的要求,反设应为:存在x1,x2∈[0,1]且x1≠x2,虽然|f(x1)-f(x2)|<|x1-x2|,但|f(x1)-f(x2)|≥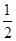

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 都是正实数,且
都是正实数,且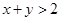 .求证:
.求证: 与
与 中至少有一个成立.
中至少有一个成立.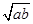 .
. ,且
,且 ,求证:
,求证:
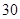 个互异的实数,可以排成
个互异的实数,可以排成 行
行 列的矩形数阵,右图所示的
列的矩形数阵,右图所示的 行
行 列的矩形数阵就是其中之一.将
列的矩形数阵就是其中之一.将 ,并设其中最小的数为
,并设其中最小的数为 ;把每列中最小的数选出,记为
;把每列中最小的数选出,记为 ,并设其中最大的数为
,并设其中最大的数为 .
.
 中至少有一个小于2。
中至少有一个小于2。 (
( 是互不相等的实数),三条抛物线至少有一条与
是互不相等的实数),三条抛物线至少有一条与 轴有两个交点.
轴有两个交点. ,
, ,并且对于任意
,并且对于任意 ,
, 成立. 猜想
成立. 猜想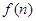 的表达式为
的表达式为


