题目内容
(本题满分13分)定义在R上的函数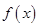 满足:对任意实数
满足:对任意实数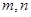 ,总有
,总有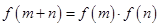 ,且当
,且当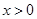 时,
时,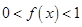 .
.
(1)试求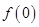 的值;
的值;
(2)判断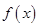 的单调性并证明你的结论;
的单调性并证明你的结论;
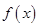 满足:对任意实数
满足:对任意实数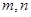 ,总有
,总有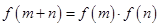 ,且当
,且当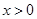 时,
时,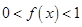 .
.(1)试求
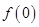 的值;
的值;(2)判断
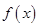 的单调性并证明你的结论;
的单调性并证明你的结论;解:(1)在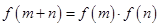 中,令
中,令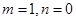 .得:
.得:
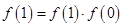 .
.
因为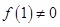 ,所以,
,所以,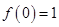 .---------------4分
.---------------4分
(2)要判断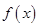 的单调性,可任取
的单调性,可任取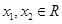 ,且设
,且设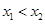 .
.
在已知条件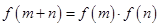 中,若取
中,若取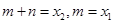 ,则已知条件可化为:
,则已知条件可化为: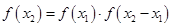 .------------------------------7分
.------------------------------7分
由于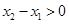 ,所以
,所以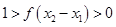 .
.
为比较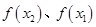 的大小,只需考虑
的大小,只需考虑 的正负即可.
的正负即可.
在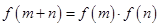 中,令
中,令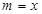 ,
, ,则得
,则得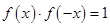 .
.
∵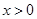 时,
时,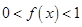 ,
,
∴ 当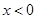 时,
时, .-----------------------11分
.-----------------------11分
又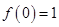 ,所以,综上,可知,对于任意
,所以,综上,可知,对于任意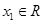 ,均有
,均有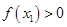 .
.
∴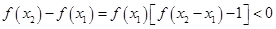 .
.
∴ 函数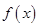 在R上单调递减.------------------------------13分
在R上单调递减.------------------------------13分
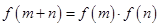 中,令
中,令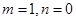 .得:
.得: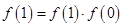 .
.因为
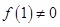 ,所以,
,所以,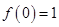 .---------------4分
.---------------4分(2)要判断
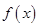 的单调性,可任取
的单调性,可任取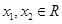 ,且设
,且设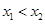 .
.在已知条件
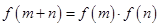 中,若取
中,若取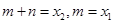 ,则已知条件可化为:
,则已知条件可化为: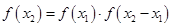 .------------------------------7分
.------------------------------7分由于
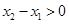 ,所以
,所以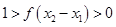 .
.为比较
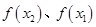 的大小,只需考虑
的大小,只需考虑 的正负即可.
的正负即可.在
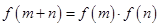 中,令
中,令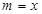 ,
, ,则得
,则得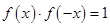 .
.∵
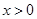 时,
时,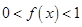 ,
,∴ 当
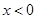 时,
时, .-----------------------11分
.-----------------------11分又
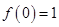 ,所以,综上,可知,对于任意
,所以,综上,可知,对于任意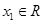 ,均有
,均有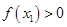 .
.∴
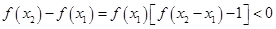 .
.∴ 函数
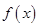 在R上单调递减.------------------------------13分
在R上单调递减.------------------------------13分略

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
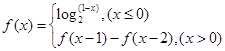 则f(2011)的值为
则f(2011)的值为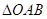 是边长为2的正三角形,记
是边长为2的正三角形,记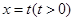 左侧的图形的面积为
左侧的图形的面积为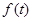 .
. 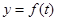 的图像;
的图像;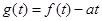 有且只有一个零点时,求
有且只有一个零点时,求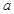 的值.
的值.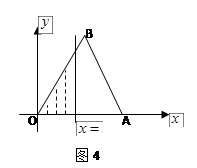
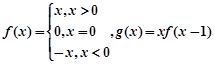 ,则函数
,则函数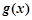 的递减区间是( )
的递减区间是( )



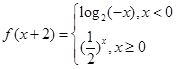 ,则
,则 =
= 、
、
 、
、
 、
、
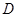 、
、
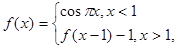 求
求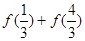 的值
的值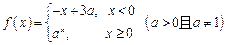 是R上的减函数,则
是R上的减函数,则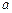 的取值范围是
的取值范围是 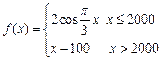 ,则
,则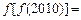 .
.