[题目]福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大.对某月即将出售的空调和冰箱进行了相关调查.得出下表:资金每台空调或冰箱所需资金月资金最多供应量空调冰箱进货成本3020300工人工资510110每台利润68问:该商场如果根据调查得来的数据.应该怎样确定空调和冰箱的月供应量.才能使商场获得的总利润最大?总利润的最大值题目和参考答案——青夏教育精英家教网—

题目内容

【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大，对某月即将出售的空调和冰箱进行了相关调查，得出下表：

资金	每台空调或冰箱所需资金（百元）		月资金最多供应量（百元）
资金	空调	冰箱	月资金最多供应量（百元）
进货成本	30	20	300
工人工资	5	10	110
每台利润	6	8

问：该商场如果根据调查得来的数据，应该怎样确定空调和冰箱的月供应量，才能使商场获得的总利润最大？总利润的最大值为多少元？

【答案】解：设每月调进空调和冰箱分别为x，y台，总利润为 z（百元）则由题意得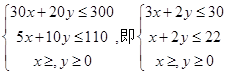

目标函数是 z=6x+8y，即y= x+
平移直线y= x，当直线过P点时，z取最大值
由得
P点坐标为P（4，9）
将（4，）代入得zmax=6×4+8×9=96（百元）
即空调和冰箱每月分别调进4台和9台是商场获得的总利润最大，总利润最大值为9600元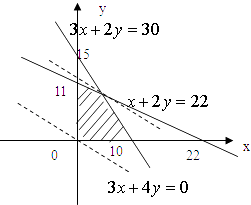

【解析】根据每月的资金供应量，我们先列出满足条件的约束条件，进而画出可行域，平移目标函数的变形直线，可得最优解．

练习册系列答案

相关题目

【题目】在平面内，定点A、B、C、D满足：| |=| |=| |， = = =﹣2，动点P、M满足：| |=1， = ，则| |的最大值是．

【题目】【南京市、盐城市2017届高三年级第二次模拟】（本小题满分16分）

如图，在平面直角坐标系xOy中，焦点在x轴上的椭圆C：＋＝1经过点(b，2e)，其中e为椭圆C的离心率．过点T(1，0)作斜率为k(k＞0)的直线l交椭圆C于A，B两点(A在x轴下方)．

（1）求椭圆C的标准方程；

（2）过点O且平行于l的直线交椭圆C于点M，N，求的值；

（3）记直线l与y轴的交点为P．若＝，求直线l的斜率k．

【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图，已知两镇分别位于东西湖岸的处和湖中小岛的处，点在的

正西方向处，．现计划铺设一条电缆联通两镇，有

两种铺设方案：①沿线段在水下铺设；②在湖岸上选一点，先沿线段在地

下铺设，再沿线段在水下铺设，预算地下、水下的电缆铺设费用分别为万元∕、

万元∕．

（1）求两镇间的距离；

（2）应该如何铺设，使总铺设费用最低？

【题目】【扬州市2016—2017学年度第一学期期末检测】（本小题满分14分）

如图，矩形ABCD是一个历史文物展览厅的俯视图，点E在AB上，在梯形BCDE区域内部展示文物，DE是玻璃幕墙，游客只能在ADE区域内参观．在AE上点P处安装一可旋转的监控摄像头，为监控角，其中M、N在线段DE（含端点）上，且点M在点N的右下方.经测量得知：AD=6米，AE=6米，AP=2米，.记（弧度），监控摄像头的可视区域PMN的面积为S平方米．