题目内容
【题目】在平面内，定点A、B、C、D满足：| 
|=| 
|=| 
|， = 
= =﹣2，动点P、M满足：| 
|=1， 
= 
，则| 
|的最大值是 ．
【答案】
【解析】解：∵| 
|=| 
|=| 
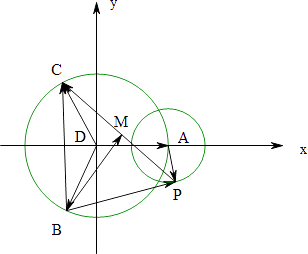
|，∴A，B，C在以D为圆心的圆D上，
∵ = 
= =﹣2，∴ 
两两夹角相等均为120°，∴|DA|=2，
以D为原点建立平面直角坐标系，设A（2，0），则B（﹣1，﹣ 
），C（﹣1， ），
∴ 
=（0，2 ）．
∵| 
|=1，∴P在以A为圆心，以1为半径的圆A上，
∵ 
= 
，∴M为PC的中点，∴ 
= 
（ 
）．
设P（2+cosα，sinα），则 
=（3+cosα，sinα+ ），
∴ =（ cosα+ 
， sinα+ 
），
∴ 
=（ cosα+ ）2+（ sinα+ ）2= 
+ sinα+ 
=3sin（α+ 
）+ ，
∴| |的最大值为 
= ．
所以答案是： ．
练习册系列答案
相关题目
【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大，对某月即将出售的空调和冰箱进行了相关调查，得出下表：
资金 | 每台空调或冰箱所需资金（百元） | 月资金最多供应量（百元） | |
空调 | 冰箱 | ||
进货成本 | 30 | 20 | 300 |
工人工资 | 5 | 10 | 110 |
每台利润 | 6 | 8 | |
问：该商场如果根据调查得来的数据，应该怎样确定空调和冰箱的月供应量，才能使商场获得的总利润最大？总利润的最大值为多少元？