题目内容
【题目】在直角坐标系![]() 中,已知动直线
中,已知动直线![]() 的参数方程:
的参数方程:![]() ,(
,(![]() 为参数,
为参数,![]() ) ,以坐标原点为极点,
) ,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 恰好有2个公共点时,求直线
恰好有2个公共点时,求直线![]() 的一般方程.
的一般方程.
【答案】(Ⅰ) 曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 或
或![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)解极坐标方程得到![]() 或
或![]() ,再化为直角坐标方程.
,再化为直角坐标方程.
(Ⅱ)由题意可知:直线![]() 与直线
与直线![]() 总有一个公共点,又
总有一个公共点,又![]() 与直线
与直线![]() 有一个切点
有一个切点![]() ,分直线
,分直线![]() 恰过点
恰过点![]() 与不过
与不过![]() 两种情况,分别求得直线
两种情况,分别求得直线![]() 的方程即可.
的方程即可.
(Ⅰ)由![]() 得
得
![]() ,
,
所以![]() 或
或![]() ,
,
即曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 或
或![]() .
.
(Ⅱ)由参数方程的意义可知:
直线![]() 过
过![]() 且倾斜角为
且倾斜角为![]() ,且
,且![]() ,
,
易知直线![]() 与直线
与直线![]() 总有一个公共点,
总有一个公共点,
又单位圆![]() 与直线
与直线![]() 有一个切点
有一个切点![]() ,
,
当直线![]() 恰过点
恰过点![]() 时,
时,
此时直线![]() 的方程为
的方程为![]() ,满足与曲线
,满足与曲线![]() 恰好有2个公共点;
恰好有2个公共点;
当直线![]() 不过点
不过点![]() 时,则
时,则![]() 与单位圆
与单位圆![]() 必相切,此时
必相切,此时![]() ,
,
设直线![]() ,则有
,则有![]() ,
,
解得![]() ,又
,又![]() ,故
,故![]() ,
,
此时直线![]() 的方程为:
的方程为:![]() ;
;
综上可得,满足条件的直线![]() 的一般方程为
的一般方程为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品.
内的产品为合格品,否则为不合格品.
注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量(克) | 频数 |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
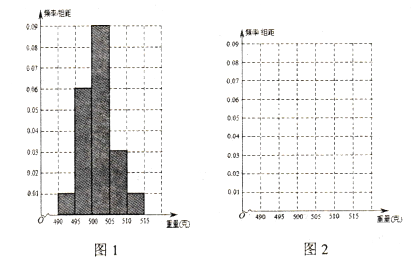
(1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
甲流水线 | 乙流水线 | 合计 | |
合格 | |||
不合格 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 5 | 25 |
经常使用手机 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则有( )的把握认为经常使用手机对数学学习成绩有影响.
参考公式: ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.97.5%B.99%C.99.5%D.99.9%