题目内容
【题目】奇函数f（x）定义域是（﹣1，0）∪（0，1），f（
）＝0，当x＞0时，总有（
x）f′（x）ln（1﹣x2）＞2f（x）成立，则不等式f（x）＞0的解集为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
把已知条件（
x）f′（x）ln（1﹣x2）＞2f（x）变形为f′（x）ln（1﹣x2）
0，可想到构造函数g（x）＝f（x）ln（1﹣x2）并判断其单调性，结合f（
）＝f（
）＝0，得g（）＝g（）＝0，由单调性可得，在（﹣1，），（0，）上，g（x）＜0，而ln（1﹣x2）＜0，则f（x）＞0成立，答案可求．
∵当x＞0时，总有（x）f′（x）ln（1﹣x2）＞2f（x）成立，即f′（x）ln（1﹣x2）
成立，也就是f′（x）ln（1﹣x2）0成立，
又∵ln（1﹣x2）＝ln（1﹣x）+ln（1+x），
∴
，即[f（x）ln（1﹣x2）]′＞0恒成立，
可知函数g（x）＝f（x）ln（1﹣x2）在（0，1）上单调递增，
∵f（x）是奇函数，∴g（x）＝f（x）ln（1﹣x2）是奇函数，则在（﹣1，0）上单调递增，
又f（）＝f（）＝0，∴g（）＝f（）＝0，
∴g（x）的图象如下：
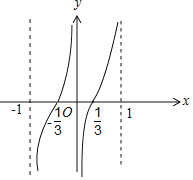
在（﹣1，），（0，）上，g（x）＜0，而ln（1﹣x2）＜0，∴f（x）＞0成立．
∴不等式f（x）＞0的解集为
．
故选：B．
练习册系列答案
计算高手系列答案
相关题目
