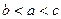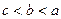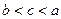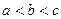题目内容
(本题满分12分)
已知函数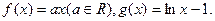
(1)若函数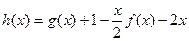 存在单调递减区间,求a的取值范围;
存在单调递减区间,求a的取值范围;
(2)当a>0时,试讨论这两个函数图象的交点个数.
已知函数
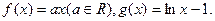
(1)若函数
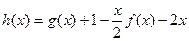 存在单调递减区间,求a的取值范围;
存在单调递减区间,求a的取值范围;(2)当a>0时,试讨论这两个函数图象的交点个数.
(1)a>1
(2)有且仅有两个交点
(2)有且仅有两个交点
(1)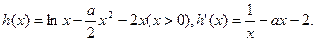
若使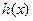 存在单调递减区间,则
存在单调递减区间,则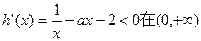 上有解.……1分
上有解.……1分
而当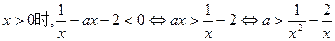
问题转化为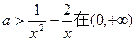 上有解,故a大于函数
上有解,故a大于函数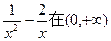 上的最小值.
上的最小值.
………………3分
又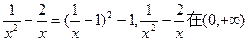 上的最小值为-1,所以a>1.……4分
上的最小值为-1,所以a>1.……4分
(2)令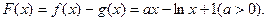
函数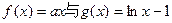 的交点个数即为函数
的交点个数即为函数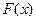 的零点的个数.……5分
的零点的个数.……5分
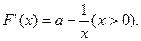
令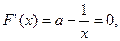 解得
解得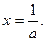
随着x的变化,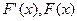 的变化情况如下表:
的变化情况如下表:
…………7分
①当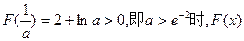 恒大于0,函数
恒大于0,函数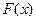 无零点.……8分
无零点.……8分
②当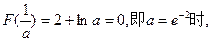 由上表,函数
由上表,函数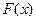 有且仅有一个零点.
有且仅有一个零点.
……9分
③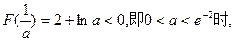 显然
显然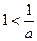
 内单调递减,
内单调递减,
所以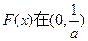 内有且仅有一个零点 …………10分
内有且仅有一个零点 …………10分
当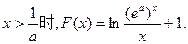
由指数函数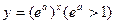 与幂函数
与幂函数 增长速度的快慢,知存在
增长速度的快慢,知存在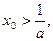
使得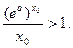
从而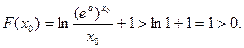
因而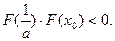
又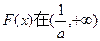 内单调递增,
内单调递增,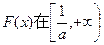 上的图象是连续不断的曲线,
上的图象是连续不断的曲线,
所以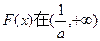 内有且仅有一个零点. …………11分
内有且仅有一个零点. …………11分
因此,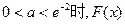 有且仅有两个零点.
有且仅有两个零点.
综上,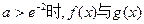 的图象无交点;当
的图象无交点;当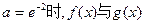 的图象有且仅有一个交点;
的图象有且仅有一个交点;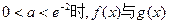 的图像有且仅有两个交点.……12分
的图像有且仅有两个交点.……12分
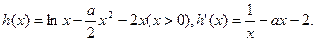
若使
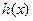 存在单调递减区间,则
存在单调递减区间,则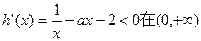 上有解.……1分
上有解.……1分而当
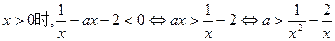
问题转化为
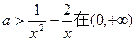 上有解,故a大于函数
上有解,故a大于函数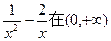 上的最小值.
上的最小值.………………3分
又
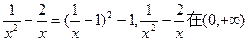 上的最小值为-1,所以a>1.……4分
上的最小值为-1,所以a>1.……4分(2)令
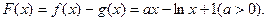
函数
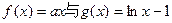 的交点个数即为函数
的交点个数即为函数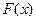 的零点的个数.……5分
的零点的个数.……5分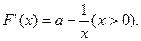
令
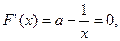 解得
解得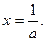
随着x的变化,
 的变化情况如下表:
的变化情况如下表: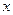 | 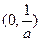 | 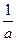 | 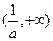 |
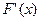 | - | 0 | + |
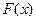 | 单调递减 | 极(最)小值2+lna | 单调递增 |
①当
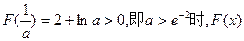 恒大于0,函数
恒大于0,函数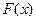 无零点.……8分
无零点.……8分②当
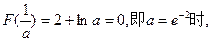 由上表,函数
由上表,函数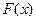 有且仅有一个零点.
有且仅有一个零点.……9分
③
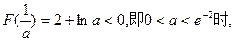 显然
显然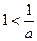
 内单调递减,
内单调递减,所以
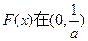 内有且仅有一个零点 …………10分
内有且仅有一个零点 …………10分当
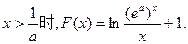
由指数函数
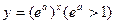 与幂函数
与幂函数 增长速度的快慢,知存在
增长速度的快慢,知存在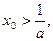
使得
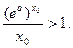
从而
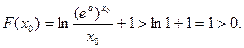
因而
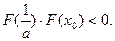
又
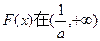 内单调递增,
内单调递增,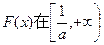 上的图象是连续不断的曲线,
上的图象是连续不断的曲线,所以
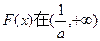 内有且仅有一个零点. …………11分
内有且仅有一个零点. …………11分因此,
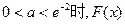 有且仅有两个零点.
有且仅有两个零点.综上,
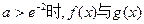 的图象无交点;当
的图象无交点;当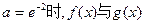 的图象有且仅有一个交点;
的图象有且仅有一个交点;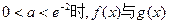 的图像有且仅有两个交点.……12分
的图像有且仅有两个交点.……12分
练习册系列答案
相关题目
 ,
, 的最大值是( )
的最大值是( )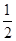
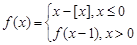 ,其中
,其中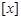 表示不超过
表示不超过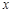 的最大整数,如
的最大整数,如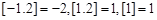 ,若
,若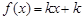 有三个不同的根,则实数
有三个不同的根,则实数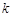 的取值范围是( )
的取值范围是( )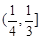
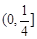
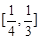
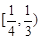
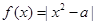 在区间[-1,1]上的最大值
在区间[-1,1]上的最大值 的最小值是 ( )
的最小值是 ( )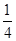

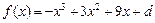 。
。 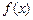 的单调区间;
的单调区间; 上的最小值为
上的最小值为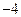 ,求实数
,求实数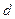 以及在该区间上的最大值.
以及在该区间上的最大值.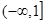 上为减函数,则m的取值范围( )
上为减函数,则m的取值范围( )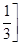
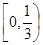
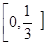
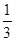 )
)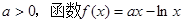
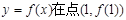 处的切线为
处的切线为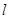 ,若
,若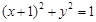 相切,求a的值
相切,求a的值 的单调区间
的单调区间 与
与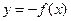 的图像关于原点对称,且
的图像关于原点对称,且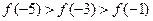 ,则
,则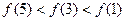
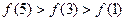
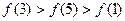
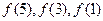 的大小关系不确定
的大小关系不确定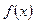 是R上的偶函数,且在区间
是R上的偶函数,且在区间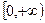 上是增函数.令
上是增函数.令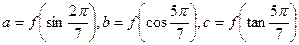 ,则
,则