题目内容
18.设Sn是正项数列{an}的前n项和,且an和Sn满足4Sn=(1+an)2(n=1,2,…),求{an}的通项公式.分析 由4Sn=(1+an)2,得4Sn-1=(1+an-1)2,两式相减得到an-an-1=2,由此能求出{an}的通项公式.
解答 解:∵Sn是正项数列{an}的前n项和,且an和Sn满足4Sn=(1+an)2(n=1,2,…),
∴4Sn=(1+an)2,①
4Sn-1=(1+an-1)2,n≥2,②
①-②,得:4an=${{a}_{n}}^{2}-{{a}_{n-1}}^{2}+2{a}_{n}-2{a}_{n-1}$,n≥2
∴(an+an-1)(an-an-1)-2(an+an-1)=0,n≥2,
(an+an-1)(an-an-1-2)=0,
∵an>0,∴an-an-1=2,
当n=1时,$4{S}_{1}=4{a}_{1}=(1+{a}_{1})^{2}$,解得a1=1,
∴{an}是首项为1,公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
点评 本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
9.已知f(x)为R上的增函数,则满足f($\frac{1}{x}$)<f(1)的实数x的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(1,+∞) |
 ,则
,则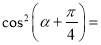 ____________.
____________.