题目内容
甲乙两支球队进行总决赛,比赛采用五场三胜制,即若有一队先胜三场,则此队为总冠军,比赛就此结束,因两队实力相当,每场比赛两队获胜的可能性均为二分之一,据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比一场增加10万元.
(Ⅰ)求总决赛中获得门票总收入恰好为220万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为x,求x的分布列和数学期望E(x).
(Ⅰ)求总决赛中获得门票总收入恰好为220万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为x,求x的分布列和数学期望E(x).
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)由已知得总决赛进行了4场比赛,甲队胜的概率为:P甲=
(
)2(
)1•
=
,乙队胜的概率为:P乙=
(
)2(
)1•
=
,由此能求出总决赛中获得门票总收入恰好为220万元的概率.
(Ⅱ)由已知得X=150,220,300,分别求出相应的概率,由此能求出x的分布列和数学期望E(x).
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
(Ⅱ)由已知得X=150,220,300,分别求出相应的概率,由此能求出x的分布列和数学期望E(x).
解答:
解:(Ⅰ)∵220=40+50+60+70,
∴总决赛进行了4场比赛,
甲队胜的概率为:P甲=
(
)2(
)1•
=
,
乙队胜的概率为:P乙=
(
)2(
)1•
=
,
∴总决赛中获得门票总收入恰好为220万元的概率:
P=P甲+P乙=
+
=
.
(Ⅱ)由已知得X=150,220,300,
P(X=150)=2×(
)3=
,
P(X=220)=
(
)4=
,
P(X=300)=2×
(
)5=
,
∴X的分布列为:
EX=150×
+220×
+300×
=232.5.
∴总决赛进行了4场比赛,
甲队胜的概率为:P甲=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
乙队胜的概率为:P乙=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
∴总决赛中获得门票总收入恰好为220万元的概率:
P=P甲+P乙=
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| 8 |
(Ⅱ)由已知得X=150,220,300,
P(X=150)=2×(
| 1 |
| 2 |
| 1 |
| 4 |
P(X=220)=
| 2×C | 1 3 |
| 1 |
| 2 |
| 3 |
| 8 |
P(X=300)=2×
| C | 2 4 |
| 1 |
| 2 |
| 3 |
| 8 |
∴X的分布列为:
| X | 150 | 220 | 300 | ||||||
| P |
|
|
|
| 1 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
满足{a,b}∪B={a,b,c}的集合B的个数是( )
| A、1 | B、2 | C、3 | D、4 |
若a,b,c成等比数列,则函数y=ax2+bx+
的图象与x轴交点个数是( )
| c |
| 4 |
| A、0 | B、1 | C、2 | D、0或2 |
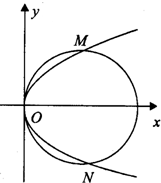 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且