题目内容
已知函数y=f(x),x∈D,y∈A;g(x)=x2-(4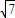 tanθ)x+1,
tanθ)x+1,(1)当f(x)=sin(x+φ)为偶函数时,求φ的值.
(2)当f(x)=sin(2x+
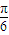 )+
)+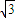 sin(2x+
sin(2x+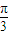 )时,g(x)在A上是单调递减函数,求θ的取值范围.
)时,g(x)在A上是单调递减函数,求θ的取值范围.(3)当f(x)=m•sin(ωx+φ1)时,(其中m∈R且m≠0,ω>0),函数f(x)的图象关于点(
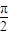 ,0)对称,又关于直线x=π成轴对称,试探讨ω应该满足的条件.
,0)对称,又关于直线x=π成轴对称,试探讨ω应该满足的条件.
【答案】分析:(1)由函数f(x)=sin(x+φ)为偶函数,可得 2sinxcosφ=0,故cosφ=0,由此可得φ 的值.
(2)化简 函数f(x)的解析式为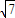 sin(2x+α)∈[-
sin(2x+α)∈[-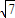 ,
,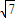 ],A=[-
],A=[-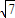 ,
,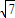 ].化简g(x)=
].化简g(x)=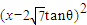 +1-28tan2θ,由题意可知:2
+1-28tan2θ,由题意可知:2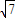 tanθ≥
tanθ≥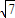 ,tanθ≥
,tanθ≥ ,由此可得θ的取值范围.
,由此可得θ的取值范围.
(3)由条件得 (2n-1)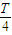 =π-
=π-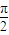 ,再由n∈N*,(2n-1)
,再由n∈N*,(2n-1)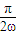 =
= ,可得ω=2n-1.由f(x)的图象关于点(
,可得ω=2n-1.由f(x)的图象关于点(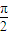 ,0)对称求得ωx+φ1 =kπ+
,0)对称求得ωx+φ1 =kπ+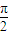 ,可得φ1 =kπ+
,可得φ1 =kπ+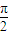 .再由f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,可得 πφ+kπ+
.再由f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,可得 πφ+kπ+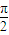 =k′π+
=k′π+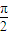 ,k′∈z,由此求得ω 满足的条件.
,k′∈z,由此求得ω 满足的条件.
解答:解:(1)因为函数f(x)=sin(x+φ)为偶函数,所以,sin(x+φ)=sin(-x+φ),
化简为 2sinxcosφ=0,∴cosφ=0,所以φ=kπ+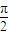 ,k∈z…(4分)
,k∈z…(4分)
(2)∵函数f(x)=sin(2x+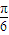 )+
)+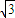 sin(2x+
sin(2x+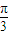 )=
)=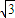 sin2x+2cos2x=
sin2x+2cos2x=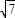 sin(2x+α)∈[-
sin(2x+α)∈[- ,
,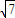 ],
],
其中,sinα=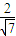 ,cosα=
,cosα=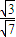 ,所以 A=[-
,所以 A=[-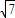 ,
,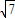 ]…(8分)
]…(8分)
g(x)=x2-(4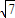 tanθ)x+1=
tanθ)x+1=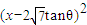 +1-28tan2θ,
+1-28tan2θ,
由题意可知:2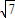 tanθ≥
tanθ≥ ,tanθ≥
,tanθ≥ ,∴kπ+arctan
,∴kπ+arctan ≤θ≤kπ+
≤θ≤kπ+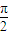 ,k∈z,
,k∈z,
即θ的取值范围是[kπ+arctan ,kπ+
,kπ+ ],k∈z.(10分)
],k∈z.(10分)
(3)由f(x)的图象关于点(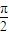 ,0)对称,又关于直线x=π成轴对称,故(2n-1)
,0)对称,又关于直线x=π成轴对称,故(2n-1)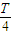 =π-
=π-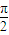 .…(12分)
.…(12分)
再由n∈N*,(2n-1)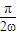 =
=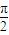 ,所以,ω=2n-1,①(14分)
,所以,ω=2n-1,①(14分)
由f(x)的图象关于点(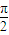 ,0)对称知道 sin(
,0)对称知道 sin(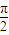 ω+φ1)=0,∴ωx+φ1 =kπ+
ω+φ1)=0,∴ωx+φ1 =kπ+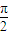 ,
,
∴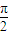 (2n-1)+φ1 =kπ,k∈z,φ1 =kπ+
(2n-1)+φ1 =kπ,k∈z,φ1 =kπ+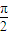 .
.
又因为f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,
∴πφ+kπ+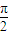 =k′π+
=k′π+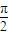 ,k′∈z,所以,ω=k,k∈N* ②.(16分)
,k′∈z,所以,ω=k,k∈N* ②.(16分)
由①②可知,ω=2n-1,n∈N*. (18分)
点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,由函数y=Asin(ωx+φ)的部分图象求解析式,
属于中档题.
(2)化简 函数f(x)的解析式为
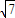 sin(2x+α)∈[-
sin(2x+α)∈[-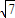 ,
,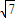 ],A=[-
],A=[-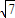 ,
,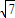 ].化简g(x)=
].化简g(x)=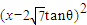 +1-28tan2θ,由题意可知:2
+1-28tan2θ,由题意可知:2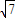 tanθ≥
tanθ≥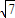 ,tanθ≥
,tanθ≥ ,由此可得θ的取值范围.
,由此可得θ的取值范围.(3)由条件得 (2n-1)
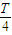 =π-
=π-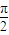 ,再由n∈N*,(2n-1)
,再由n∈N*,(2n-1)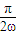 =
= ,可得ω=2n-1.由f(x)的图象关于点(
,可得ω=2n-1.由f(x)的图象关于点(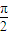 ,0)对称求得ωx+φ1 =kπ+
,0)对称求得ωx+φ1 =kπ+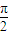 ,可得φ1 =kπ+
,可得φ1 =kπ+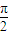 .再由f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,可得 πφ+kπ+
.再由f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,可得 πφ+kπ+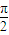 =k′π+
=k′π+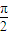 ,k′∈z,由此求得ω 满足的条件.
,k′∈z,由此求得ω 满足的条件.解答:解:(1)因为函数f(x)=sin(x+φ)为偶函数,所以,sin(x+φ)=sin(-x+φ),
化简为 2sinxcosφ=0,∴cosφ=0,所以φ=kπ+
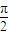 ,k∈z…(4分)
,k∈z…(4分)(2)∵函数f(x)=sin(2x+
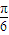 )+
)+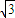 sin(2x+
sin(2x+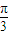 )=
)=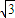 sin2x+2cos2x=
sin2x+2cos2x=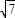 sin(2x+α)∈[-
sin(2x+α)∈[- ,
,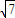 ],
],其中,sinα=
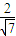 ,cosα=
,cosα=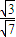 ,所以 A=[-
,所以 A=[-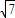 ,
,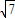 ]…(8分)
]…(8分)g(x)=x2-(4
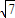 tanθ)x+1=
tanθ)x+1=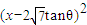 +1-28tan2θ,
+1-28tan2θ,由题意可知:2
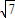 tanθ≥
tanθ≥ ,tanθ≥
,tanθ≥ ,∴kπ+arctan
,∴kπ+arctan ≤θ≤kπ+
≤θ≤kπ+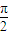 ,k∈z,
,k∈z,即θ的取值范围是[kπ+arctan
 ,kπ+
,kπ+ ],k∈z.(10分)
],k∈z.(10分)(3)由f(x)的图象关于点(
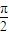 ,0)对称,又关于直线x=π成轴对称,故(2n-1)
,0)对称,又关于直线x=π成轴对称,故(2n-1)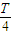 =π-
=π-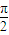 .…(12分)
.…(12分)再由n∈N*,(2n-1)
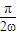 =
=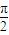 ,所以,ω=2n-1,①(14分)
,所以,ω=2n-1,①(14分)由f(x)的图象关于点(
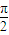 ,0)对称知道 sin(
,0)对称知道 sin(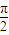 ω+φ1)=0,∴ωx+φ1 =kπ+
ω+φ1)=0,∴ωx+φ1 =kπ+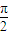 ,
,∴
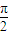 (2n-1)+φ1 =kπ,k∈z,φ1 =kπ+
(2n-1)+φ1 =kπ,k∈z,φ1 =kπ+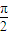 .
.又因为f(x)的图象关于直线x=π成轴对称,所以 sin(πω+φ1 )=±1,
∴πφ+kπ+
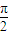 =k′π+
=k′π+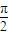 ,k′∈z,所以,ω=k,k∈N* ②.(16分)
,k′∈z,所以,ω=k,k∈N* ②.(16分)由①②可知,ω=2n-1,n∈N*. (18分)
点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,由函数y=Asin(ωx+φ)的部分图象求解析式,
属于中档题.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足