Question

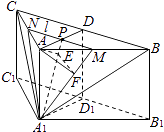
【题目】如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB=AC=2AA1 ， ∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD的中点．

（1）在平面ABC内，试做出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；
（2）设（1）中的直线l交AB于点M，交AC于点N，求二面角A﹣A1M﹣N的余弦值．

Answer 1

【答案】
（1）解：在平面ABC内，过点P作直线l∥BC

∵直线l平面A1BC，BC平面A1BC，

∴直线l∥平面A1BC，

∵△ABC中，AB=AC，D是BC的中点，

∴AD⊥BC，结合l∥BC得AD⊥l

∵AA1⊥平面ABC，l平面ABC，∴AA1⊥l

∵AD、AA1是平面ADD1A1内的相交直线

∴直线l⊥平面ADD1A1；

（2）解：连接A1P，过点A作AE⊥A1P于E，过E点作EF⊥A1M于F，连接AF

由（I）知MN⊥平面A1AE，结合MN平面A1MN得平面A1MN⊥平面A1AE，

∵平面A1MN∩平面A1AE=A1P，AE⊥A1P，∴AE⊥平面A1MN，

∵EF⊥A1M，EF是AF在平面A1MN内的射影，

∴AF⊥A1M，可得∠AFE就是二面角A﹣A1M﹣N的平面角

设AA1=1，则由AB=AC=2AA1，∠BAC=120°，可得∠BAD=60°，AB=2且AD=1

又∵P为AD的中点，∴M是AB的中点，得AP= ，AM=1

Rt△A1AP中，A1P= = ；Rt△A1AM中，A1M=

∴AE= = ，AF= =

∴Rt△AEF中，sin∠AFE= = ，可得cos∠AFE= =

即二面角A﹣A1M﹣N的余弦值等于 ．

【解析】（1）在平面ABC内过点P作直线l∥BC，根据线面平行的判定定理得直线l∥平面A1BC．由等腰三角形“三线合一”得到AD⊥BC，从而得到AD⊥l，结合AA1⊥l且AD、AA1是平面ADD1A1内的相交直线，证出直线l⊥平面ADD1A1；（2）连接A1P，过点A作AE⊥A1P于E，过E点作EF⊥A1M于F，连接AF．根据面面垂直判定定理，证出平面A1MN⊥平面A1AE，从而得到AE⊥平面A1MN，结合EF⊥A1M，由三垂线定理得AF⊥A1M，可得∠AFE就是二面角A﹣A1M﹣N的平面角．设AA1=1，分别在Rt△A1AP中和△AEF中算出AE、AF的长，在Rt△AEF中，根据三角函数的定义算出sin∠AFE的值，结合同角三角函数的平方关系算出cos∠AFE的值，从而得出二面角A﹣A1M﹣N的余弦值．
【考点精析】通过灵活运用直线与平面垂直的判定，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题．