题目内容
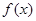 是定义在R上的偶函数,当
是定义在R上的偶函数,当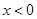 时,
时,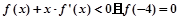 ,则不等式
,则不等式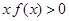 的解集为( )
的解集为( )| A.(-4,0)∪(4,+∞) | B.(-4,0)∪(0,4) |
| C.(-∞,-4)∪(4,+∞) | D.(-∞,-4)∪(0,4) |
D
记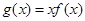 ,则
,则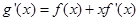 ,依题意可得,当
,依题意可得,当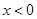 时
时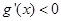 ,此时函数
,此时函数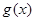 单调递减。
单调递减。
因为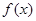 是定义在R上的偶函数,所以
是定义在R上的偶函数,所以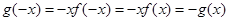 ,故
,故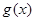 在R上是奇函数。
在R上是奇函数。
根据奇函数的图象性质可得,当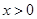 时,
时,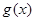 也单调递减
也单调递减
因为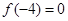 ,所以
,所以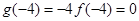
则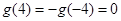
而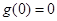 ,所以根据
,所以根据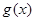 的单调性可得,
的单调性可得,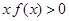 即
即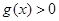 的解集为
的解集为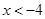 或
或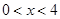 ,故选D。
,故选D。
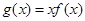 ,则
,则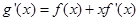 ,依题意可得,当
,依题意可得,当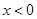 时
时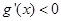 ,此时函数
,此时函数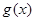 单调递减。
单调递减。因为
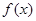 是定义在R上的偶函数,所以
是定义在R上的偶函数,所以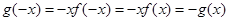 ,故
,故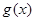 在R上是奇函数。
在R上是奇函数。根据奇函数的图象性质可得,当
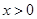 时,
时,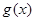 也单调递减
也单调递减因为
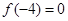 ,所以
,所以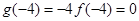
则
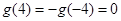
而
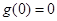 ,所以根据
,所以根据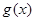 的单调性可得,
的单调性可得,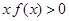 即
即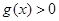 的解集为
的解集为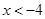 或
或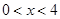 ,故选D。
,故选D。
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
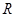 上的函数
上的函数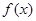 满足
满足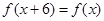 .当
.当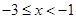 时,
时,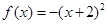 ,当
,当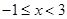 时,
时,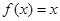 。则
。则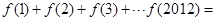
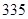
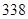
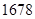
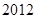
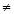 1,F(x)为偶函数,则G(x)=F(x)·log
1,F(x)为偶函数,则G(x)=F(x)·log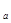 (x+
(x+ )是_______函数(填“奇”或“偶”),它的图像关于______对称。
)是_______函数(填“奇”或“偶”),它的图像关于______对称。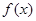 是定义在
是定义在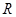 上的奇函数,当
上的奇函数,当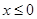 时,
时,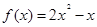 ,则
,则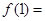 ( )
( )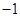
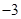
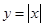
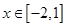 ,求函数的最小值与最大值
,求函数的最小值与最大值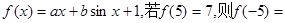
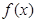 是定义在
是定义在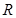 上的奇函数,当
上的奇函数,当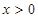 时,
时,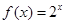 ,则
,则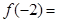 ___________.
___________.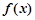 是偶函数,当
是偶函数,当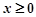 时,
时, 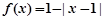 ,满足
,满足 的实数
的实数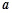 的个数为_____________个
的个数为_____________个