题目内容
【题目】已知函数f(x)=loga ![]() (a>0,a≠1).
(a>0,a≠1).
(1)当a>1时,讨论f(x)的奇偶性,并证明函数f(x)在(1,+∞)上为单调递减;
(2)当x∈(n,a﹣2)时,是否存在实数a和n,使得函数f(x)的值域为(1,+∞),若存在,求出实数a与n的值,若不存在,说明理由.
【答案】
(1)解:f(x)的定义域为{x|x<﹣1或x>1},关于原点对称,
又f(﹣x)= ![]() ,∴f(x)为奇函数,
,∴f(x)为奇函数,
证明:当a>1时,设1<x1<x2,则
f(x1)﹣f(x2)= ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() >1,又a>1,∴loga
>1,又a>1,∴loga ![]() >0,则f(x1)>f(x2),
>0,则f(x1)>f(x2),
∴函数f(x)在(1,+∞)上为减函数
(2)解:令 ![]() =
= ![]() ,x∈(n,a﹣2),
,x∈(n,a﹣2),
①当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),
令 ![]() ,解得
,解得 ![]() .∴x∈(1,
.∴x∈(1, ![]() ).
).
故有 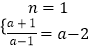 ,解得
,解得 ![]() ;
;
②当0<a<1时,t∈(0,a),则x∈( ![]() ),∴
),∴ 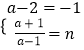 ,(不合题意).
,(不合题意).
综上所述,存在实数n=1,a= ![]() ,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞)
,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞)
【解析】(1)直接利用函数单调性与奇偶性的定义判断;(2)令 ![]() =
= ![]() ,x∈(n,a﹣2),当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),令
,x∈(n,a﹣2),当a>1时,要使f(x)的值域为(1,+∞),则须t∈(a,+∞),令 ![]() ,解得
,解得 ![]() .可得x∈(1,
.可得x∈(1, ![]() ).则
).则 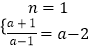 ,解得
,解得 ![]() ;当0<a<1时,t∈(0,a),则x∈(
;当0<a<1时,t∈(0,a),则x∈( ![]() ),得
),得 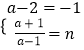 ,(不合题意).由此可得存在实数n=1,a=
,(不合题意).由此可得存在实数n=1,a= ![]() ,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞).
,当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞).
【考点精析】掌握奇偶性与单调性的综合是解答本题的根本,需要知道奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.

【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)