题目内容
【题目】函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
【答案】B
【解析】解:设g(x)=xf(x),则g′(x)=xf′(x)+f(x),
∵当x<0时,xf′(x)+f(x)>0,
∴则当x<0时,g′(x)>0,
∴函数g(x)=xf(x)在(﹣∞,0)上为增函数,
∵函数f(x)是奇函数,∴g(﹣x)=(﹣x)f(﹣x)=(﹣x)[﹣f(x)]=xf(x)=g(x),
∴函数g(x)为定义域上的偶函数,
由f(1)=0得,g(1)=0,函数g(x)的图象大致如右图:
∵不等式f(x)<0![]() <0,
<0,
∴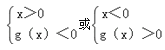
由函数的图象得,﹣1<x<0或x>1,
∴使得f(x)<0成立的x的取值范围是:(﹣1,0)∪(1,+∞),
故选:B.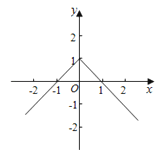
根据题意构造函数g(x)=xf(x),由求导公式和法则求出g′(x),结合条件判断出g′(x)的符号,即可得到函数g(x)的单调区间,根据f(x)奇函数判断出
g(x)是偶函数,将不等式进行转化,由图象求出不等式成立时x的取值范围.

练习册系列答案
相关题目