题目内容
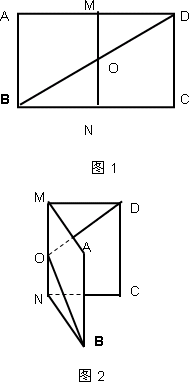
已知平面α和平面β交于直线l,P是空间一点,PA⊥α,垂足为A,PB⊥β,垂足B,且PA=1,PB=2,若点A在β内的射影与点B在α内的射影重合,则点P到l的距离为分析:根据点A在β内的射影与点B在α内的射影重合,得出α⊥β,设射影为点C,从而得到点P到l的距离为PC的长,又因为PC为矩形PACB的对角线,从而解决问题.
解答:解∵点A在β内的射影与点B在α内的射影重合,∴α⊥β
设射影为点C,点P到l的距离为PC的长,
而PC为矩形PACB的对角线
∴PC=
.
则点P到l的距离为
.
故答案为:
.
设射影为点C,点P到l的距离为PC的长,
而PC为矩形PACB的对角线
∴PC=
| 5 |
则点P到l的距离为
| 5 |
故答案为:
| 5 |
点评:本题考查面面垂直,点、线、面间的距离计算,考查学生计算能力,逻辑思维能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
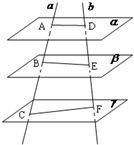 如图,已知平面α,β,γ,且α∥β∥γ,直线a,b分别与平面α,β,γ交于点A,B,C和D,E,F,若AB=1,BC=2,DF=9,则EF=
如图,已知平面α,β,γ,且α∥β∥γ,直线a,b分别与平面α,β,γ交于点A,B,C和D,E,F,若AB=1,BC=2,DF=9,则EF=