题目内容
10.已知函数f(x)=ex-ax2+(a-e+1)x-1,(e=2.71828…是自然对数的底数,a为常数).(Ⅰ) 当a=0时,求f(x)的单调区间;
(Ⅱ)若函数g(x)=f(x)-$\frac{1}{2}$x•f′(x)在区间[1,+∞)上单调递减,求a的范围
(Ⅲ)当a∈(e-2,1)时,函数f(x)=ex-ax2+(a-e+1)x-1在区间(0,1)上是否有零点?并说明理由.
分析 (Ⅰ)当a=0时,求出f(x),然后求f′(x),根据导数符号即可求出f(x)的单调区间;
(Ⅱ)求出g(x),求g′(x),g″(x),根据g″(x)的符号可判断导函数g′(x)单调递减,从而便有g′(x)≤g′(1),再根据g(x)在[1,+∞)上单调递减,从而g′(x)≤g′(1)≤0,这样即可求得a的范围;
(Ⅲ)先假设f(x)存在零点,从而得到f(x)=0成立,根据f(x)=0可解出a=$\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}$,这时候令h(x)=$\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}$,只要证明e-2<h(x)<1即可:先证h(x)<1,作差h(x)-1=$\frac{{e}^{x}-{x}^{2}+(2-e)x-1}{{x}^{2}-x}$,容易判断x2-x<0,从而只要证明ex-x2+(2-e)x-1>0,可令H(x)=ex-x2+(2-e)x-1,通过求H′(x),H″(x),便能判断函数H(x)在(0,1)上的单调性,再根据H(0)=0,H(1)=0即可说明H(x)>0成立,同样的办法证明h(x)>e-2即可.
解答 解:(Ⅰ)当a=0时,f(x)=ex+(1-e)x-1,f′(x)=ex+(1-e);
∴f(x)的单调增区间为(ln(e-1),+∞),f(x)的单调减区间为(-∞,ln(e-1));
(Ⅱ)$g(x)=(1-\frac{1}{2}x){e}^{x}+\frac{1}{2}(a-e+1)x-1$,$g′(x)=\frac{1}{2}(1-x){e}^{x}+\frac{1}{2}(a-e+1)$;
∴$g″(x)=-\frac{1}{2}x{e}^{x}$,x∈[1,+∞);
∴g″(x)<0,∴g′(x)在[1,+∞)上单调递减;
又g(x)在[1,+∞)上单调递减;
∴$g′(x)≤g′(1)=\frac{1}{2}(a-e+1)≤0$;
∴a≤e-1;
∴a的范围为(-∞,e-1];
(Ⅲ)假设函数f(x)在区间(0,1)上有零点;
即存在x∈(0,1),使得ex-ax2+(a-e+1)x-1=0;
即$a=\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}$,记$h(x)=\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}$;
①若h(x)<1,∴$\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}-1<0$,即:
$\frac{{e}^{x}-{x}^{2}+(2-e)x-1}{{x}^{2}-x}<0$;
由于x∈(0,1),有x2-x<0;
即证ex-x2+(2-e)x-1>0在x∈(0,1)恒成立;
令H(x)=ex-x2+(2-e)x-1,x∈(0,1);
H′(x)=ex-2x+2-e,H″=ex-2;
当x∈(0,ln2),H″(x)<0,当x∈(ln2,1),H″(x)>0;
∴当x∈(0,ln2),H′(x)单调递减,x∈(ln2,1),H′(x)单调递增;
而H′(0)=1-0+2-e>0,H′(1)=e-2+2-e=0,H′(ln2)=eln2-2ln2+2-e=4-e-2ln2<0;
故在(0,ln2)上存在唯一的实数x0使得H′(x0)=0;
所以,在(0,x0)上H(x)单调递增,在(x0,1)上H(x)单调递减;
而H(0)=0,H(1)=0;
故H(x)>0在(0,1)成立;
即$h(x)=\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}<1$成立;
②若h(x)>e-2;
∴$\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}-(e-2)>0$,即$\frac{{e}^{x}-(e-2){x}^{2}-x-1}{{x}^{2}-x}>0$;
由于x∈(0,1),有x2-x<0;
即证ex-(e-2)x2-x-1<0在x∈(0,1)恒成立;
令H(x)=ex-(e-2)x2-x-1,H′(x)=ex-2(e-2)x-1,H″(x)=ex-2(e-2);
当x∈(0,ln2(e-2)),H″(x)<0,H′(x)单调递减;当x∈(ln2(e-2),1),H″(x)>0,H′(x)单调递增;
而H′(0)=0,H′(1)=3-e>0;
∴在(ln2(e-2),1)上存在唯一的实数x0使得H′(x0)=0;
所以,在(0,x0)上H(x)单调递减,在(x0,1)上H(x)单调递增;
又H(0)=0,H(1)=0;
故H(x)<0在(0,1)成立,即$h(x)=\frac{{e}^{x}+(1-e)x-1}{{x}^{2}-x}>e-2$成立.
由①②可得,a∈(e-2,1)时,h(x)存在零点.
点评 考查根据函数导数符号求函数单调区间的方法,函数导数符号和函数单调性的关系,函数单调性定义的运用,会正确求导,会求二阶导数并能运用二阶导数,函数零点的概念,以及掌握本题在证明函数存在零点时用到的方法.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{11π}{6}$ |
| A. | 3x-2y-13=0 | B. | 3x-2y-13=0或x-2y-3=0 | ||
| C. | x-2y-3=0 | D. | x-2y-3=0或2x+3y-13=0 |
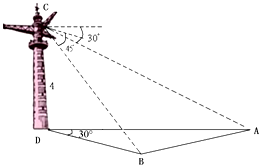 如图,跳伞塔CD高4,在塔顶测得地面上两点A,B的俯角分别是30°,45°,又测得∠ADB=30°,求AB两地的距离.
如图,跳伞塔CD高4,在塔顶测得地面上两点A,B的俯角分别是30°,45°,又测得∠ADB=30°,求AB两地的距离.