题目内容
已知函数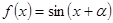 ,
, 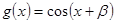 ,
,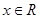 ,
,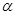 、
、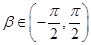 .
.
(Ⅰ)若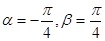 ,判断
,判断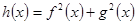 的奇偶性;
的奇偶性;
(Ⅱ) 若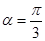 ,
,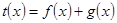 是偶函数,求
是偶函数,求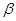 ;
;
(Ⅲ)是否存在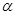 、
、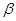 ,使得
,使得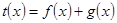 是奇函数但不是偶函数?若存在,试确定
是奇函数但不是偶函数?若存在,试确定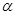 与
与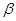 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
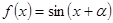 ,
, 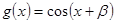 ,
,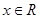 ,
,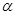 、
、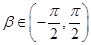 .
.(Ⅰ)若
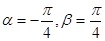 ,判断
,判断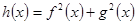 的奇偶性;
的奇偶性;(Ⅱ) 若
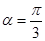 ,
,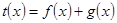 是偶函数,求
是偶函数,求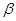 ;
;(Ⅲ)是否存在
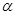 、
、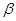 ,使得
,使得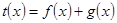 是奇函数但不是偶函数?若存在,试确定
是奇函数但不是偶函数?若存在,试确定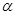 与
与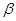 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.(Ⅰ)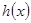 是非奇非偶函数.(Ⅱ)
是非奇非偶函数.(Ⅱ)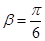 ;(Ⅲ)存在
;(Ⅲ)存在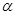 、
、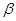 满足
满足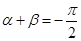 时,
时,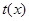 是奇函数但不是偶函数.
是奇函数但不是偶函数.
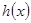 是非奇非偶函数.(Ⅱ)
是非奇非偶函数.(Ⅱ)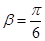 ;(Ⅲ)存在
;(Ⅲ)存在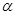 、
、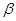 满足
满足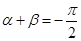 时,
时,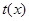 是奇函数但不是偶函数.
是奇函数但不是偶函数.试题分析:(Ⅰ) 方法一(定义法):
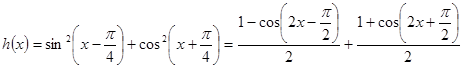
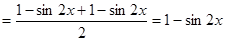 . 2分
. 2分所以
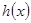 是非奇非偶函数. 3分
是非奇非偶函数. 3分方法二(特殊值法):由
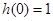 知
知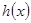 不是奇函数. 1分
不是奇函数. 1分又由
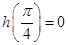 ,
,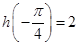 知
知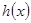 不是偶函数. 2分
不是偶函数. 2分所以
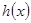 是非奇非偶函数. 3分
是非奇非偶函数. 3分(Ⅱ) 方法一(定义法):
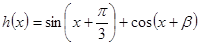 ,
,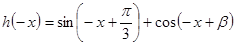
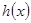 偶函数,
偶函数,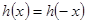 ,
,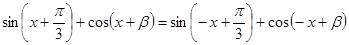
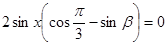 , 5分
, 5分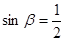 ,
, 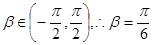 . 6分
. 6分 方法二(特殊值法):
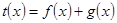 为偶函数
为偶函数所以
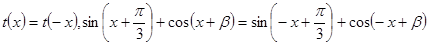
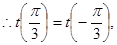 所以
所以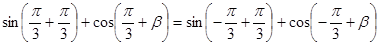 5分
5分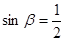 ,
,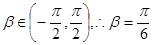 ,经验证
,经验证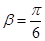 满足题意. 6分
满足题意. 6分(Ⅲ)方法一:假设存在
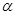 、
、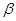 ,使得
,使得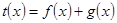 是奇函数.
是奇函数.由
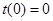 得,
得,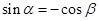 ,所以
,所以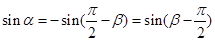 .
.由
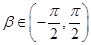 知,
知,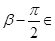
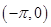 .
.又
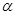
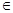
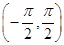 ,故
,故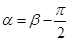 或
或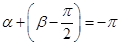 ,
,即
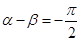 或
或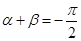 . 8分
. 8分当
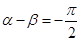 时,
时,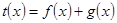 =
=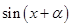 +
+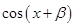
=
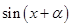 +
+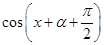 =
=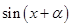 -
-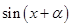 =0,
=0,此时
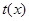 既是奇函数又是偶函数.不合题意,舍去. 9分
既是奇函数又是偶函数.不合题意,舍去. 9分当
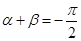 时,
时,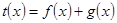 =
=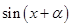 +
+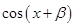
=
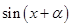 +
+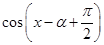 =
=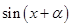 -
- =
=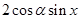
此时
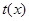 是奇函数但不是偶函数.
是奇函数但不是偶函数.综上,存在
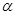 、
、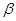 满足
满足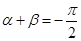 时,
时,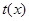 是奇函数但不是偶函数. 10分
是奇函数但不是偶函数. 10分方法二:假设存在
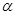 、
、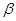 ,使得
,使得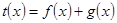 是奇函数.
是奇函数.由
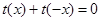 得,
得,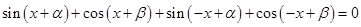
化简整理得,
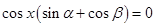 ,从而
,从而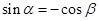 .下同方法一.
.下同方法一.点评:(1)此题主要考查三角函数的奇偶性。判断一个函数奇偶性的步骤:一求函数的定义域,看定义域是否关于原点对称;二判断
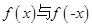 。有时,若
。有时,若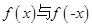 的关系不好判断时,可以根据定义域进行化简。(2) 若函数
的关系不好判断时,可以根据定义域进行化简。(2) 若函数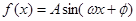 为偶函数,则
为偶函数,则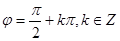 ;若函数
;若函数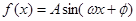 为奇函数,则
为奇函数,则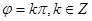 。
。
练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目

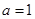
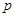 :
: 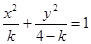 表示焦点在
表示焦点在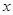 轴上的椭圆,命题
轴上的椭圆,命题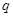 :
: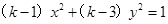 表示双曲线。若
表示双曲线。若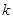 的取值范围。(10分)
的取值范围。(10分)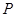 :
: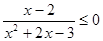 ;则
;则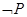 命题是;
命题是;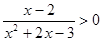 ;
;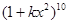 (
(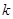 为正整数)的展开式中,
为正整数)的展开式中,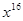 的系数小于90,则
的系数小于90,则 .若记
.若记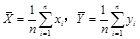 ,则回归直线
,则回归直线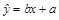 必过点
必过点 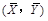 ;
;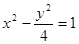 的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;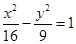 与椭圆
与椭圆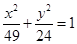 有相同的焦点;
有相同的焦点;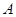 、
、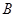 为两个定点,
为两个定点,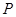 为动点,且
为动点,且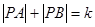 ,其中常数
,其中常数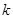 为正实数,则动点
为正实数,则动点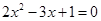 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;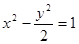 的右焦点
的右焦点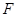 作直线
作直线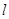 交双曲线于
交双曲线于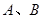 两点,若
两点,若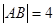 ,则这样的直线
,则这样的直线 ,其中
,其中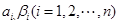 均为常数,下列说法正确的有
均为常数,下列说法正确的有 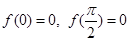 ,则对于任意
,则对于任意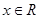 ,
,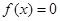 恒成立;
恒成立;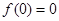 ,则
,则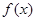 是奇函数; (3) 若
是奇函数; (3) 若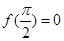 ,则
,则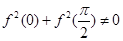 ,且当
,且当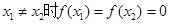 ,则
,则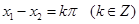 ;
;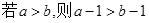 ”的否命题是 ( )
”的否命题是 ( ) 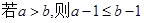
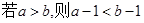
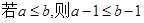
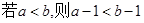
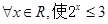 ”的否定是“
”的否定是“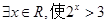 ”;
”;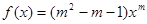 是幂函数,且在
是幂函数,且在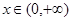 上为增函数,则
上为增函数,则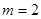 ;
;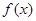 在
在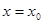 处有极值,则
处有极值,则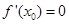 ”的否命题是真命题;
”的否命题是真命题;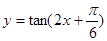 在区间
在区间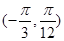 上单调递增;
上单调递增;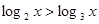 ”是“
”是“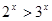 ”成立的充要条件。
”成立的充要条件。