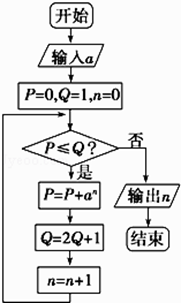
题目内容
【题目】己知函数f(x)= ![]() (其中e为自然对数的底数),h(x)=x﹣
(其中e为自然对数的底数),h(x)=x﹣ ![]() .
.
(I)求函数f(x)的单调区间;
(II)设g(x)= ![]() ,.已知直线y=
,.已知直线y= ![]() 是曲线y=f(x)的切线,且函数g(x)在(0,+∞)上是增函数.
是曲线y=f(x)的切线,且函数g(x)在(0,+∞)上是增函数.
(i)求实数a的值;
(ii)求实数c的取值范围.
【答案】解:(Ⅰ)∵ ![]() ,
,
∴ ![]() ,
,
①当a>0时,
在x∈(﹣∞,0)∪(2,+∞)时,f'(x)<0,在x∈(0,2)时,f'(x)>0,
故f(x)在(﹣∞,0),(2,+∞)上是减函数,在(0,2)上是增函数;
②当a<0时,
在x∈(﹣∞,0)∪(2,+∞)时,f'(x)>0,在x∈(0,2)时,f'(x)<0,
故f(x)在(﹣∞,0),(2,+∞)上是增函数,在(0,2)上是减函数;
(Ⅱ)(i)对f(x)求导,得 ![]() ,
,
设直线 ![]() 与曲线y=f(x)切于点P(x0,y0),
与曲线y=f(x)切于点P(x0,y0),
则 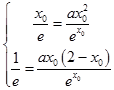 解得a=x0=1,∴a=1
解得a=x0=1,∴a=1
(ii)记函数(x)=f(x)﹣h(x)= ![]() ,x>0,
,x>0,
求导,得 ![]() ,
,
当x≥2时,'(x)<0恒成立,
当0<x<2时, ![]() ,
,
∴ ![]() ,
,
∴'(x)<0在(0,+∞)上恒成立,故(x)在(0,+∞)上单调递减.
又 ![]() ,
, ![]() ,
,
曲线(x)=f(x)﹣h(x)在[1,2]上连续不间断,
∴由函数的零点存在性定理及其单调性知,唯一的x0∈(1,2),使(x0)=0.
∴当x∈(0,x0)时,(x)>0,当x∈(x0,+∞)时,(x)<0.
∴当x>0时, ![]() =
= 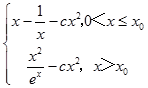
求导,得 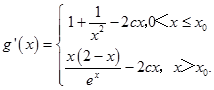
由函数g(x)在(0,+∞)上是增函数,且曲线y=g(x)在(0,+∞)上连续不断知:
g'(x)≥0在(0,x0],(x0,+∞)上恒成立.
①当x∈(x0,+∞)时, ![]() ﹣2cx≥0在(x0,+∞)上恒成立,
﹣2cx≥0在(x0,+∞)上恒成立,
即 ![]() 在(x0,+∞)上恒成立,
在(x0,+∞)上恒成立,
记 ![]() ,x>x0,则
,x>x0,则 ![]() ,x>x0,
,x>x0,
当 x变化时,u'(x),u(x)变化情况列表如下:
x | (x0,3) | 3 | (3,+∞) |
u'(x) | ﹣ | 0 | + |
u(x) | ↓ | 极小值 | ↑ |
∴u(x)min=u(x)极小值=u(3)= ![]() ,
,
故“ ![]() 在(x0,+∞)上恒成立”,只需2c≤u(x)min=
在(x0,+∞)上恒成立”,只需2c≤u(x)min= ![]() ,即
,即 ![]() .
.
②当x∈(0,x0]时,g'(x)=1+ ![]() ﹣2cx,
﹣2cx,
当c≤0时,g'(x)>0在x∈(0,x0]上恒成立,
综合①②知,当 ![]() 时,函数g(x)在(0,+∞)上是增函数.
时,函数g(x)在(0,+∞)上是增函数.
故实数c的取值范围是 ![]()
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)(i)根据切线方程求出a的值即可;(ii)问题转化为 ![]() 在(x0,+∞)上恒成立,根据函数的单调性求出c的范围即可.
在(x0,+∞)上恒成立,根据函数的单调性求出c的范围即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).