题目内容
2．已知集合M=$\{x|y={x^{\frac{1}{2}}}\}，N=\{x|-1＞2-3x≤5\}$，U=R，则图中阴影部分表示的集合是[-1，0）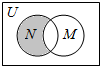
分析 图中阴影部分表示的集合是（∁UM）∩N，分别求出M，N，可得答案．
解答 解：∵集合$\{x|y={x}^{\frac{1}{2}}\}=[0，+∞）$，N={x|-1＞2-3x≤5}=[-1，1），
图中阴影部分表示的集合是（∁UM）∩N=（-∞，0）∩[-1，1）=[-1，0），
故答案为：[-1，0）
点评 本题考查的知识点是集合的交集，并集，补集运算，难度不大，属于基础题．
练习册系列答案
相关题目
如图，设A是棱长为2的正方体的一个顶点，过从顶点A出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，截去8个三棱锥，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：
如图，在平面直角坐标系中，锐角α和钝角β的终边分别与单位圆交于A，B两点，
14．与双曲线$\frac{y^2}{4}-{x^2}$=1有共同的渐近线，且过点（2，2）的双曲线标准方程为（ ）
| A． | $\frac{y^2}{3}-\frac{x^2}{12}=1$ | B． | $\frac{x^2}{3}-\frac{y^2}{12}=1$ | C． | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | D． | $\frac{x^2}{2}-\frac{y^2}{8}=1$ |
11．
已知某几何体的三视图如图所示，其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆，则该几何体的表面积为（ ）
已知某几何体的三视图如图所示，其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆，则该几何体的表面积为（ ）| A． | 8-π | B． | 8+π | C． | 8-2π | D． | 8+2π |