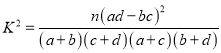题目内容
【题目】已知x＞0，y＞0，且x+y=1，求：
（1）x2+y2的最小值；
（2）
+ 
+ 
的最小值．
【答案】
（1）解： 
，当且仅当x=y= 
．表达式取得最小值
（2）解：∵x+y=1，∴ 
，∴ 
．∴ 
+ 
+ 
= 
．当且仅当x=y= ．表达式的最小值为：6．
【解析】（1）利用重要不等式求解表达式的最小值即可．（2）利用已知条件求出xy的最值，然后化简所求的表达式，利用基本不等式求解最小值即可．
【考点精析】本题主要考查了基本不等式和基本不等式在最值问题中的应用的相关知识点，需要掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
；用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能正确解答此题．
同步练习河南大学出版社系列答案【题目】漳州水仙鳞茎硕大，箭多花繁，色美香郁，素雅娟丽，有“天下水仙数漳州”之美誉．现某水仙花雕刻师受雇每天雕刻250粒水仙花，雕刻师每雕刻一粒可赚1.2元，如果雕刻师当天超额完成任务，则超出的部分每粒多赚0.5元；如果当天未能按量完成任务，则按完成的雕刻量领取当天工资．
（Ⅰ）求雕刻师当天收入（单位：元）关于雕刻量
（单位：粒， 
）的函数解析式
；
（Ⅱ）该雕刻师记录了过去10天每天的雕刻量
（单位：粒），整理得下表：
雕刻量 | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率．
（ⅰ）求该雕刻师这10天的平均收入；
（ⅱ）求该雕刻师当天的收入不低于300元的概率.
【题目】某大学为调研学生在
， 
两家餐厅用餐的满意度，从在
， 
两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分.
整理评分数据，将分数以10为组距分成6组： 
， 
， 
， 
， 
， 
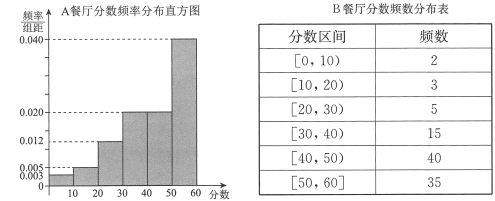
，得到
餐厅分数的频率分布直方图，和
餐厅分数的频数分布表：
定义学生对餐厅评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 |
|
|
|
（Ⅰ）在抽样的100人中，求对
餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在， 
两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对
餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从
， 
两家餐厅中选择一家用餐，你会选择哪一家？说明理由.
