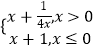题目内容
【题目】在四棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ,底面
,底面 ![]() 是梯形,
是梯形, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)设 ![]() 为棱
为棱 ![]() 上一点,
上一点, ![]() ,试确定
,试确定 ![]() 的值使得二面角
的值使得二面角 ![]() 为
为 ![]() .
.
【答案】
(1)解:∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
, ![]() ,在梯形
,在梯形 ![]() 中,过点作
中,过点作 ![]() 作
作 ![]() 于
于 ![]() ,
,
在 ![]() 中,
中, ![]() ,又在
,又在 ![]() 中,
中, ![]() ,
,
∴ ![]() , ∵
, ∵ ![]() ,
, ![]() ,
, ![]() ,
,![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,∵
,∵ ![]() 平面
平面 ![]() ,
,
∴ ![]() ,∵
,∵ ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,∴平面
,∴平面 ![]() 平面
平面 ![]() ;
;
(2)解:
过点 ![]() 作
作 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 于点
于点 ![]() ,连
,连 ![]() ,由(1)可知
,由(1)可知 ![]() 平面
平面 ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() 是二面角
是二面角 ![]() 的平面角,
的平面角,
∴ ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,由(1)知
,由(1)知 ![]() ,∴
,∴ ![]() ,又∵
,又∵ ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,∵
,∵ ![]() ,∴
,∴ ![]()
![]() ;法二:以
;法二:以 ![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为 ![]() ,
, ![]() ,
, ![]() 轴建立空间直角坐标系(如图)
轴建立空间直角坐标系(如图)
则 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,令
,令 ![]() ,则
,则![]() ,
, ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,∵
,∵ ![]() 平面
平面 ![]() ,∴
,∴ ![]() 是平面
是平面 ![]() 的一个法向量,
的一个法向量,
设平面 ![]() 的法向量为
的法向量为 ![]() ,则
,则  ,即
,即 ![]() 即
即  ,
,
不妨令 ![]() ,得
,得 ![]() ,∵二面角
,∵二面角 ![]() 为
为 ![]() ,
,
∴  ,解得
,解得 ![]() , ∵
, ∵ ![]() 在棱
在棱 ![]() 上,∴
上,∴ ![]() ,故
,故 ![]() 为所求.
为所求.
【解析】(1)在梯形ABCD中,过点作B作BH⊥CD于H,通过面面垂直的判定定理即得结论;
(2)过点Q作QM∥BC交PB于点M,过点M作MN⊥BD于点N,连QN.则∠QNM是二面角Q-BD-P的平面角,在Rt三角形MNQ中利用tan∠MNQ=![]() 计算即可.
计算即可.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程 ![]() ;
;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y﹣0.05x2﹣1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 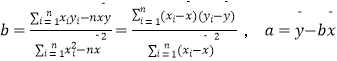 )
)
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() (1)=
(1)= ![]() +1.1,方程乙:
+1.1,方程乙: ![]() (2)=
(2)= ![]() +1.6.
+1.6.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() =yi﹣
=yi﹣ ![]() ,
, ![]() 称为相应于点(xi , yi)的残差(也叫随机误差);
称为相应于点(xi , yi)的残差(也叫随机误差);
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | ﹣0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和Q1及Q2 , 并通过比较Q1 , Q2的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入﹣成本).