题目内容
【题目】已知函数f(x)=-x2-2x,g(x)= 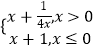
(1)求g[f(1)]的值;
(2)若方程g[f(x)]-a=0有4个实数根,求实数a的取值范围.
【答案】
(1)解:利用解析式直接求解得g[f(1)]=g(-3)=-3+1=-2.
(2)解:令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t在t∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象,由图象可知,当1≤a< ![]() 时,函数y=g(t)(t<1)与y=a有2个不同的交点,即所求a的取值范围是
时,函数y=g(t)(t<1)与y=a有2个不同的交点,即所求a的取值范围是 ![]() .
.
【解析】由题意可得函数y=g[f(x)]与函数y=a有4个交点,结合图象可得实数a的取值范围.根的存在问题相对来说是零点里头最重要的一个点,也是比较常考的点,一般都是以中档题的形式在选择题里出现,在解这种题的时候,做出函数图象是首要选择,然后根据图形去寻找答案.

练习册系列答案
相关题目