题目内容
抛物线 :
: 的焦点与双曲线
的焦点与双曲线 :
: 的右焦点的连线交
的右焦点的连线交 于第一象限的点
于第一象限的点 ,若
,若 在点
在点 处的切线平行于
处的切线平行于 的一条渐近线,则
的一条渐近线,则 ( )
( )
A.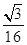 | B. | C. | D. |
B
解析试题分析:经过第一象限的双曲线的渐近线为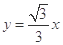 ,抛物线的焦点为
,抛物线的焦点为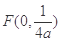 ,双曲线的右焦点为
,双曲线的右焦点为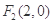 ,设M(
,设M(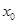 ,
,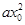 ),则
),则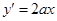 ,所以曲线
,所以曲线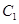 在M点的切线斜率为
在M点的切线斜率为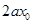 ,由题知
,由题知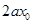 =
=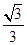 ,所以
,所以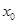 =
=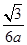 ,因为三点
,因为三点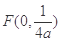 ,
,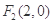 ,
,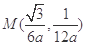 共线,所以
共线,所以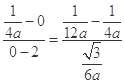 ,即
,即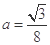 ,故选B.
,故选B.
考点:双曲线的性质,抛物线的性质,导数的几何意义,三点共线的充要条件,两直线平行的充要条件

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 是抛物线
是抛物线 上任意一点,则当
上任意一点,则当 点到直线
点到直线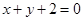 的距离最小时,
的距离最小时, 点与该抛物线的准线的距离是
点与该抛物线的准线的距离是
| A.2 | B.1 | C. | D. |
设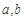 是关于t的方程
是关于t的方程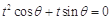 的两个不等实根,则过
的两个不等实根,则过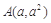 ,
,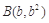 两点的直线与双曲线
两点的直线与双曲线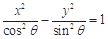 的公共点的个数为
的公共点的个数为
| A.3 | B.2 | C.1 | D.0 |
双曲线 的渐近线与圆
的渐近线与圆 相切,则双曲线离心率为( ).
相切,则双曲线离心率为( ).
A. | B.2 | C. | D.3 |
过双曲线 的左焦点
的左焦点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,双曲线左顶点为
,双曲线左顶点为 ,若
,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.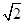 | B. | C.3 | D.2 |
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线 上至少取两个点,将其坐标记录于下表中:
上至少取两个点,将其坐标记录于下表中:
| x | 5 | - | 4 |  |  |
| y | 2 | 0 | -4 |  | - |

(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,-
 )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.  上,且与直线
上,且与直线 相切,被直线
相切,被直线 截得的弦长为
截得的弦长为 ,求圆C的方程.
,求圆C的方程. ,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1:2的两部分,则双曲线的离心率为( )
,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1:2的两部分,则双曲线的离心率为( )



 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( ) B.
B. C.2 D.
C.2 D.