题目内容
15．若0＜a＜b，求证：（a2+b2）（a-b）＞（a2-b2）（a+b）分析 通过作差可知（a2+b2）（a-b）-（a2-b2）（a+b）=2ab（b-a），利用0＜a＜b可知ab＞0、b-a＞0，进而计算可得结论．
解答 证明：∵（a2+b2）（a-b）-（a2-b2）（a+b）
=（a3+ab2-a2b-b3）-（a3-ab2+a2b-b3）
=2ab2-2a2b
=2ab（b-a），
∵0＜a＜b，
∴ab＞0，b-a＞0，
∴2ab（b-a）＞0，
∴（a2+b2）（a-b）＞（a2-b2）（a+b）．
点评 本题考查不等式的证明，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
10．已知复数z=i2013+（i+1）5，则z的虚部是（ ）
| A． | 4 | B． | 3 | C． | -4 | D． | -3 |
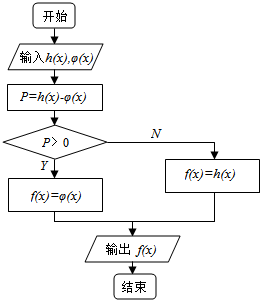函数f（x）的定义由程序框图给出，程序运行时，输入h（x）=（$\frac{1}{2}$）x，φ（x）=log2x，则f（$\frac{1}{2}$）+f（4）的值为-$\frac{15}{16}$．