题目内容

4．如图，已知正四棱台上、下底面边长分别为4和8，侧棱长为8，求它的侧面积．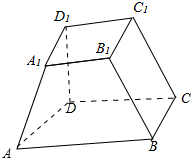

分析 正棱台的侧面积公式S棱台侧=$\frac{1}{2}$（C1+C2）h'，其中C1、C2分别是上下底的周长，h'是棱台的斜高．由此在侧面等腰梯形中，计算出棱台的斜高的长度，再结合公式可求出此棱台的侧面积．

解答 解：作出一个侧面等腰梯形的高，也是棱台的斜高，
则由等腰梯形的性质，可得斜高h'=$\sqrt{{8}^{2}-{（\frac{8-4}{2}）}^{2}}$=$2\sqrt{15}$，

再用棱台侧面积公式，得棱台的侧面积为S侧=$\frac{1}{2}$（4+8）×2$\sqrt{15}$×4=48$\sqrt{15}$．

点评 本题给出正三棱台棱台上下底面边长和侧棱长，求三棱台的侧面积，着重考查了正棱台的侧面积公式，属于基础题．

练习册系列答案
相关题目
14．已知函数f（x）是周期为2的函数，当-1≤x≤1时，f（x）=$\left\{\begin{array}{l}{{x}^{2}，-1≤x＜0}\\{kx-1，0≤x≤1}\end{array}\right.$，则f（$\frac{17}{4}$）=（　　）
A．0B．-$\frac{1}{2}$C．$\frac{1}{2}$D．-$\frac{1}{4}$
15．若0＜a＜b，求证：（a2+b2）（a-b）＞（a2-b2）（a+b）
12．已知数列{an}是公比为正整数的等比数列，若a2=2且a1，a3+$\frac{1}{2}$，a4成等差数列，
（Ⅰ）求数列{an}的通项an；
（Ⅱ）定义：$\frac{n}{{{P_1}+{P_2}+…+{P_n}}}$为n个正数P1，P2，P3，…，Pn（ n∈N*）的“均倒数”，
（ⅰ）若数列{bn}前n项的“均倒数”为$\frac{1}{{2{a_n}-1}}$（n∈N*），求数列{bn}的通项bn；
（ⅱ）试比较$\frac{1}{b_1}$+$\frac{2}{b_2}$+…+$\frac{n}{b_n}$与2的大小，并说明理由．
19．若正四棱锥底面边长为1，侧面积是底面积的2倍，则它的体积为（　　）
A．$\frac{\sqrt{2}}{6}$B．$\frac{\sqrt{3}}{6}$C．$\frac{\sqrt{2}}{4}$D．$\frac{\sqrt{3}}{4}$
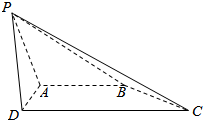9．如图，四棱锥P-ABCD中，底面ABCD为梯形，AB∥CD．AD⊥CD，CD=2AB=2AD=4，侧面PAD为正三角形，AB⊥PA．
（1）求点D到平面PAB的距离；
（2）求证：平面PBC⊥平面PCD．
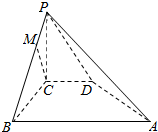16．如图所示，在四棱锥P-ABCD中，PC⊥平面ABCD，PC=2，在四边形ABCD中，∠B=∠C=90°，AB=4，CD=1，点M在PB上，PB=4PM，PB与平面ABCD成30°的角．求证：
（1）CM∥平面PAD；
（2）平面PAB⊥平面PAD．
13．过抛物线y+2x2=0的焦点的直线交抛物线于A、B两点．则xAxB=-$\frac{1}{16}$．
3．设集合A={（x，y）|logax+logay＞0}，B={（x，y）|y+x＜a}，若A∩B=∅，则a的取值范围是（　　）
A．∅B．a＞0，a≠1C．0＜a≤2，a≠1D．1＜a≤2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网