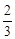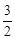题目内容
(本小题满分13分)函数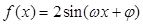
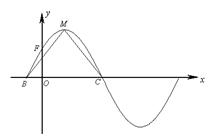
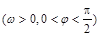 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与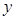 轴交于点
轴交于点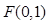 ,与
,与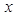 轴交于点
轴交于点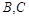 ,
,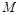 为最高点,且
为最高点,且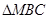 的面积为
的面积为 .
.
(Ⅰ)求函数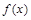 的解析式;
的解析式;
(Ⅱ)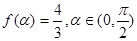 ,求
,求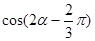 的值.
的值.
(Ⅲ)将函数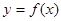 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的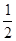 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移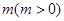 个单位,得函数
个单位,得函数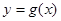 的图象,若函数
的图象,若函数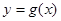 为奇函数,求
为奇函数,求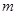 的最小值.
的最小值.
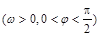 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与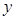 轴交于点
轴交于点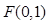 ,与
,与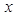 轴交于点
轴交于点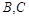 ,
,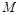 为最高点,且
为最高点,且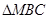 的面积为
的面积为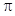 .
.
(Ⅰ)求函数
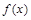 的解析式;
的解析式;(Ⅱ)
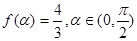 ,求
,求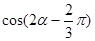 的值.
的值.(Ⅲ)将函数
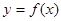 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的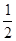 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移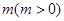 个单位,得函数
个单位,得函数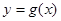 的图象,若函数
的图象,若函数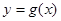 为奇函数,求
为奇函数,求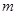 的最小值.
的最小值.(I) .
.
(Ⅱ)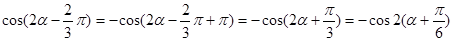 =
=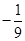 ;
;
(Ⅲ)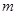 的最小值为
的最小值为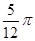 .
.
 .
.(Ⅱ)
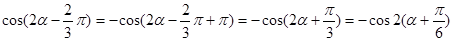 =
=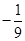 ;
;(Ⅲ)
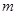 的最小值为
的最小值为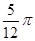 .
. 试题分析:(I)先利用
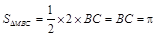 ,然后可知周期T,从而得到
,然后可知周期T,从而得到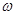 ,再根据f(0)=1,得到
,再根据f(0)=1,得到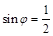 ,结合
,结合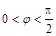 ,得到
,得到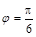 ,最终确定f(x)的解析式.
,最终确定f(x)的解析式.(II)由
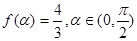 ,可得
,可得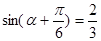 ,
,所以
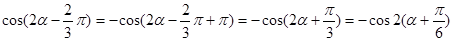 ,
,再利用余弦的二倍角公式将
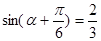 值代入即可求解.
值代入即可求解.(I)∵
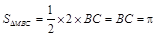 ,
,∴周期
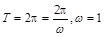 .························ 3分
.························ 3分由
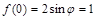 ,得
,得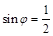 ,
,∵
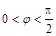 ,∴
,∴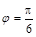 ,
,∴
 .·························· 5分
.·························· 5分(Ⅱ)∵
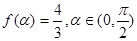 ∴
∴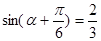 ············ 6分
············ 6分∴
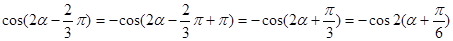
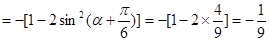 ················ 9分
················ 9分(Ⅲ)由函数
 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的 倍(纵坐标不变),得函数
倍(纵坐标不变),得函数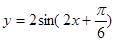 的图象,···································· 10分
的图象,···································· 10分再向左平移
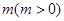 个单位,得函数
个单位,得函数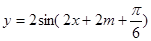 的图象
的图象即
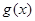
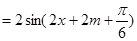 ······················ 11分
······················ 11分∵函数
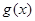 为奇函数 ∴
为奇函数 ∴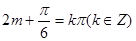 ,即
,即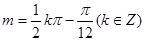
又
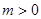 ,∴
,∴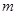 的最小值为
的最小值为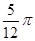 .···················· 13分
.···················· 13分 的图像及性质,
的图像及性质,点评:求三角函数
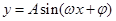 的一般步骤:先求A,
的一般步骤:先求A,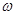 ,最后再根据特殊点求
,最后再根据特殊点求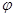 .
.本小题用到二倍角公式:
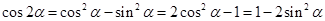 .
.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 (其中
(其中 )的图象如图所示,则
)的图象如图所示,则





 的图象如图所示,则
的图象如图所示,则 的值等于 。
的值等于 。
 (A>0,0<
(A>0,0< <
< )在一个周期内的图象如右图,此函数的解析式为___________________。
)在一个周期内的图象如右图,此函数的解析式为___________________。
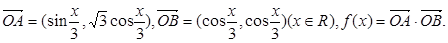
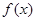 图象的对称中心的横坐标;
图象的对称中心的横坐标;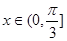 ,求函数
,求函数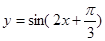 的图像向右平移
的图像向右平移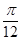 个单位后所得的图像的一个对称轴是( )
个单位后所得的图像的一个对称轴是( )
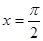
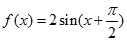 在其定义域上是( )
在其定义域上是( ) 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;  一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的? ,又
,又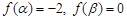 ,且
,且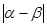 的最小值为
的最小值为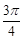 ,则正数
,则正数 的值是
的值是