题目内容
如图,正方形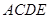 所在的平面与平面
所在的平面与平面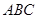 垂直,
垂直,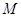 是
是 和
和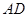 的交点,
的交点,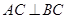 ,且
,且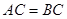 .
.
(1)求证: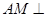 平面
平面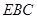 ;
;
(2)求二面角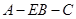 的大小.
的大小.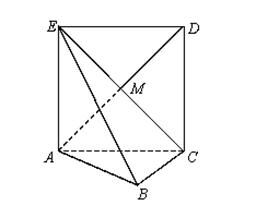
(1)详见解析;(2)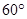 .
.
解析试题分析:(1)要证AM⊥平面EBC,关键是寻找线线垂直,利用四边形ACDE是正方形,可得AM⊥EC.利用平面ACDE⊥平面ABC,BC⊥AC,可得BC⊥平面EAC,从而有BC⊥AM.故可证;
(2)先求出二面角A-EB-C的平面角. 再在Rt△EAB中,利用AH⊥EB,有AE•AB=EB•AH.设EA=AC=BC=2a可得AB=2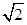 a,EB=2
a,EB=2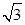 a,∴AH=
a,∴AH=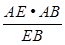 =
= .从而可求二面角A-EB-C的平面角 .
.从而可求二面角A-EB-C的平面角 .
证明:(1)∵四边形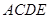 是正方形,
是正方形,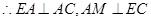
∵平面 平面
平面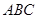 ,又∵
,又∵ ,
,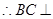 平面
平面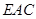 .
. 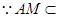 平面
平面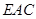 ,
,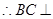
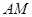 .
. 平面
平面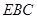 . 6分
. 6分
(2)过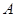 作
作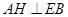 于
于 ,连结
,连结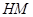 .
.
 平面
平面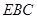 ,
,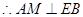 .
. 平面
平面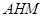 .
.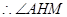 是二面角
是二面角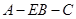 的平面角.
的平面角.
∵ 平面 平面
平面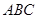 ,
, 平面
平面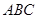 .
.
 .
.
在 中,
中, 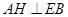 ,有
,有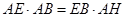 .
.
设 可得
可得 ,
,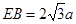 ,
, .
. 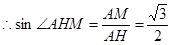 .
.  .
.
∴二面角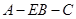 等于
等于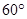 . 12分.
. 12分.
考点:1.用空间向量求直线与平面的夹角; 2.用空间向量求平面间的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
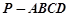 的底面
的底面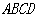 是平行四边形,
是平行四边形,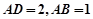 ,
,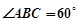 ,
, 面
面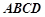 ,设
,设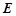 为
为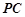 中点,点
中点,点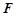 在线段
在线段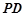 上且
上且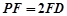 .
.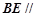 平面
平面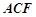 ;
;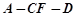 的大小为
的大小为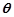 ,若
,若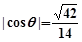 ,求
,求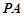 的长.
的长.
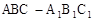 中,
中,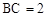 ,
,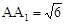 ,D、E分别是
,D、E分别是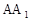 、
、 的中点,
的中点,
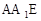 ⊥面BCD;
⊥面BCD;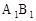 与平面BCD所成的角.
与平面BCD所成的角.
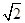 .
.

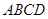 为平行四边形,
为平行四边形,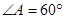 ,
,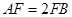 ,
,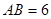 ,点
,点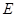 在
在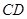 上,
上,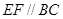 ,
, ,
,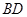 与
与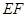 相交于
相交于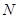 .现将四边形
.现将四边形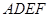 沿
沿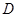 在平面
在平面 上的射影恰在直线
上的射影恰在直线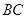 上.
上.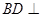 平面
平面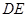 与平面
与平面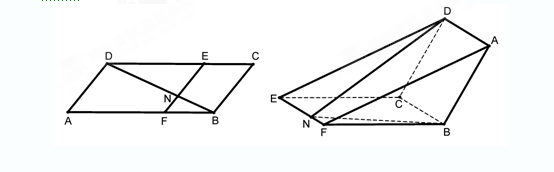
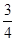 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4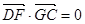 ,
,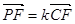 ,求
,求 的值.
的值.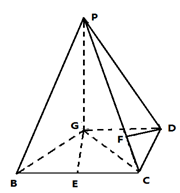
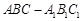 中,侧面
中,侧面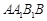 为菱形, 且
为菱形, 且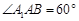 ,
, ,
, 是
是 的中点.
的中点.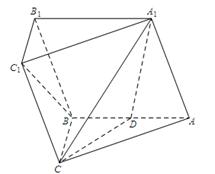
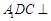 平面
平面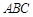 ;
; ∥平面
∥平面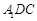 .
.