题目内容
在平面直角坐标系xOy中,设椭圆4x2+y2=1在矩阵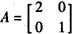 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.
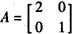 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程. 解:设P(x0,y0)是椭圆上任意一点,点P(x0,y0)在矩阵A对应的变换F变为点P′(x′0,y′0),
则有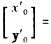
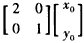 ,即
,即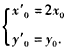 ,所以
,所以 ,
,
又因为点P在椭圆上,故4x02+y02=1,
从而(x′0)2+(y′0)2=1,
所以,曲线F的方程为x2+y2=1.
则有
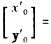
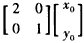 ,即
,即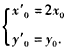 ,所以
,所以 ,
,又因为点P在椭圆上,故4x02+y02=1,
从而(x′0)2+(y′0)2=1,
所以,曲线F的方程为x2+y2=1.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是