题目内容
已知函数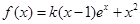 .
.
(1)当时 ,求函数
,求函数 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;
(2)若在y轴的左侧,函数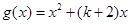 的图象恒在
的图象恒在 的导函数
的导函数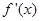 图象的上方,求k的取值范围;
图象的上方,求k的取值范围;
(3)当k≤-l时,求函数 在[k,l]上的最小值m。
在[k,l]上的最小值m。
(1) 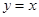 ; (2)
; (2)  ; (3)1.
; (3)1.
解析试题分析:(1) 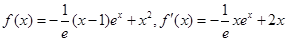 所以可求
所以可求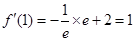
从而求得切线的方程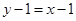 即
即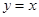 ;
;
(2) 由函数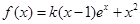 得:
得: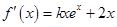 由题意
由题意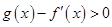 在
在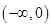 上恒成立 ;即:
上恒成立 ;即: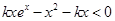
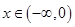
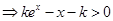 , 令
, 令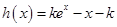
问题转化为求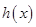 的最小值
的最小值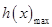 ,由
,由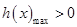 可求
可求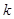 的取值范围.
的取值范围.
(3) 由于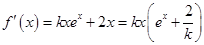 ,根据该函数的零点及
,根据该函数的零点及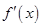 的符号判断函数
的符号判断函数 的单调性并求最小值.
的单调性并求最小值.
试题解析:
解:(1)当 时 ,
时 ,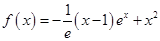 ,
,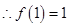 1分
1分
函数 在点
在点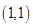 处的切线方程为
处的切线方程为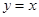 3分
3分
(2)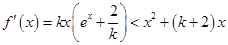
即: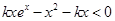
因为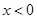 , 所以
, 所以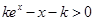 4分
4分
令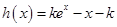 ,则
,则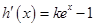 5分
5分
当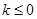 时,
时,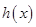 在
在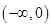 为减函数,
为减函数,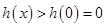 ,符合题意 6分
,符合题意 6分
当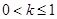 时,
时,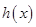 在
在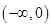 为减函数,
为减函数,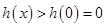 ,符合题意 7分
,符合题意 7分
当 时,
时,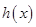 在
在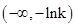 为减函数,在
为减函数,在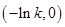 为增函数,
为增函数,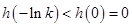 8分
8分
综上, .
.
(3)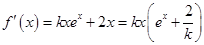 ,令
,令 ,得
,得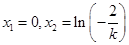 , 9分
, 9分
令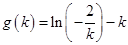 ,则
,则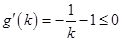
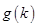 在
在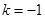 时取最小值
时取最小值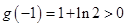
所以 10分
10分
当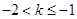

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
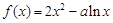 .
.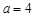 ,求函数
,求函数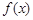 的极小值;
的极小值;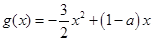 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量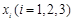 使得
使得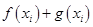 的值相等,若存在,请求出
的值相等,若存在,请求出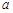 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?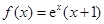 .
.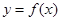 在点
在点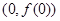 处的切线方程;
处的切线方程;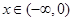 ,都有
,都有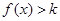 ,求
,求 的取值范围.
的取值范围.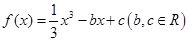 .
.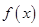 在点
在点 处的切线方程为
处的切线方程为 ,求
,求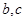 的值;
的值; ,函数
,函数 在区间
在区间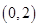 内有唯一零点,求
内有唯一零点,求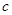 的取值范围;
的取值范围;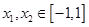 ,均有
,均有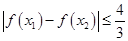 ,求
,求 的取值范围.
的取值范围.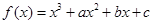 在
在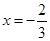 与
与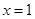 时都取得极值
时都取得极值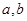 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式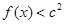 恒成立,求
恒成立,求 的取值范围
的取值范围 
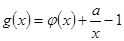 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值; ,
,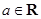 ,且
,且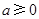 .求函数
.求函数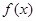 的单调递增区间.
的单调递增区间.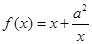 ,
, ,其中
,其中 .
. 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数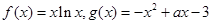 .
. 在
在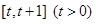 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数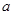 的取值范围;
的取值范围;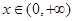 ,都有
,都有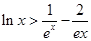 成立.
成立. 的图像与直线
的图像与直线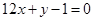 相切于点
相切于点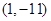 .
.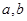 的值;
的值; 的单调性.
的单调性.