题目内容
已知函数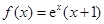 .
.
(1)求曲线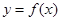 在点
在点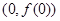 处的切线方程;
处的切线方程;
(2)若对于任意的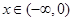 ,都有
,都有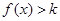 ,求
,求 的取值范围.
的取值范围.
(1)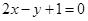 ;(2)
;(2)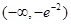 .
.
解析试题分析:(1)先对原函数进行求导得 ,则在点
,则在点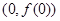 处的切线方程的斜率
处的切线方程的斜率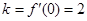 ,过点
,过点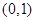 ,所以切线方程为
,所以切线方程为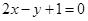 ;(2)利用求导,求出
;(2)利用求导,求出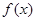 的最小值,只需要
的最小值,只需要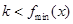 即可.对
即可.对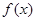 求导,列出
求导,列出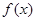 和
和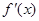 的变化情况统计表,则
的变化情况统计表,则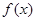 在
在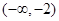 上递减,在
上递减,在 上递增,所以
上递增,所以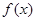 在
在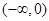 上的最小值是
上的最小值是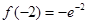 ,则
,则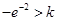 ,解得
,解得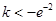 .
.
试题解析:(1) 2分
2分 ,
,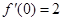 4分
4分
∴曲线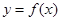 在
在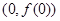 处的切线方程为
处的切线方程为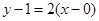 , 即
, 即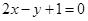 . 6分
. 6分
(2)令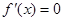 得
得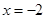 , 2分
, 2分
当 变化时,
变化时,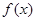 和
和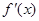 的变化情况如下表:
的变化情况如下表:
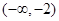
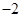

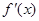



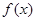
↘ 极小值 ↗
∴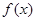 在
在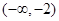 上递减,在
上递减,在 上递增 4分
上递增 4分
∴

练习册系列答案
相关题目
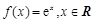 .
. 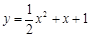 有唯一公共点.
有唯一公共点. 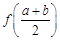 与
与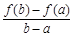 的大小, 并说明理由.
的大小, 并说明理由. 
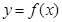 的单调区间;
的单调区间;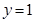 恰有两个交点,求
恰有两个交点,求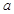 的取值范围.
的取值范围.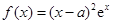 在
在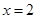 时取得极小值.
时取得极小值. 的值;
的值;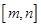 ,使得
,使得 在该区间上的值域为
在该区间上的值域为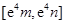 ?若存在,求出
?若存在,求出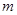 ,
,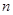 的值;
的值;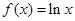 ,
,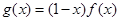
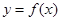 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;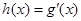 及
及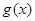 在区间
在区间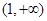 上的单调性;
上的单调性;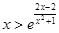 在
在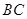 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)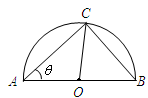
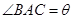 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为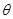 的函数
的函数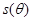 ;
;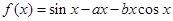
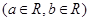 .
.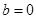 ,讨论函数
,讨论函数 在区间
在区间 上的单调性;
上的单调性;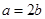 且对任意的
且对任意的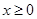 ,都有
,都有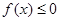 恒成立,求实数
恒成立,求实数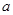 的取值范围.
的取值范围.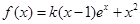 .
. ,求函数
,求函数 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;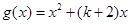 的图象恒在
的图象恒在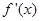 图象的上方,求k的取值范围;
图象的上方,求k的取值范围; 为函数
为函数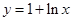 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线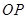 的斜率
的斜率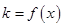 .
.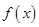 在区间
在区间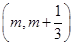
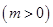 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;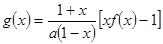 ,若对任意
,若对任意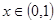 恒有
恒有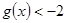 ,求实数
,求实数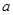 的取值范围.
的取值范围.