题目内容
已知函数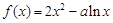 .
.
(1)若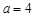 ,求函数
,求函数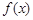 的极小值;
的极小值;
(2)设函数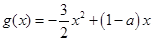 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量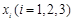 使得
使得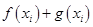 的值相等,若存在,请求出
的值相等,若存在,请求出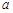 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?
(1)极小值为2;(2) 不存在,详见解析.
不存在,详见解析.
解析试题分析:(1)由a=4,得函数f(x)的解析式,求出其导函数以及导数为0的根,通过比较两根的大小找到函数的单调区间,进而求出f(x)的极小值;(2)若定义域内存在三个不同的自变量的取值xi(i=1,2,3),使得f(xi)-g(xi)的值恰好都相等,设f(xi)-g(xi)=m.(i=1,2,3),则对于某一实数m,方程f(x)-g(x)=m在(0,+∞)上有三个不等的实数,由此能求出在定义域内不存在三个不同的自变量的取值xi(i=1,2,3)使得f(xi)-g(xi)的值恰好都相等.
解:(1)定义域为 ,由已知得
,由已知得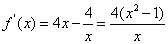 , 2分
, 2分
则当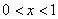 时
时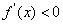 ,
,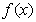 在
在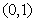 上是减函数,
上是减函数,
当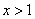 时
时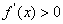 ,
,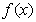 在
在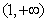 上是增函数,
上是增函数,
故函数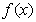 的极小值为
的极小值为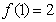 . 6分
. 6分
(2)若存在,设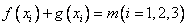 ,
,
则对于某一实数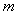 方程
方程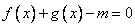 在
在 上有三个不等的实根,
上有三个不等的实根,
设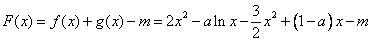 ,
,
则函数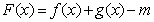 的图象与x轴有三个不同交点,
的图象与x轴有三个不同交点,
即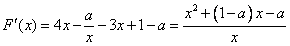 在
在 有两个不同的零点.9分
有两个不同的零点.9分
显然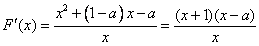 在
在 上至多只有一个零点
上至多只有一个零点
则函数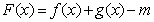 的图象与x轴至多有两个不同交点,则这样的
的图象与x轴至多有两个不同交点,则这样的 不存在。 13分
不存在。 13分
考点:1.函数在某点取得极值的条件;2.根的存在性及根的个数判断.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
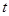 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于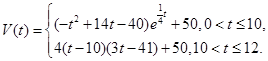
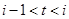 表示第1月份(
表示第1月份(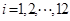 ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?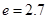 计算).
计算).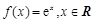 .
. 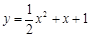 有唯一公共点.
有唯一公共点. 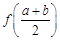 与
与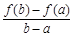 的大小, 并说明理由.
的大小, 并说明理由. 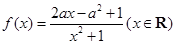 ,其中
,其中 .
.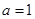 时,求曲线
时,求曲线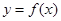 在点
在点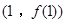 处的切线方程;
处的切线方程;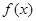 的单调区间及在
的单调区间及在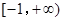 上的最大值.
上的最大值.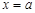 和
和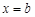 是函数
是函数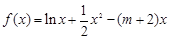 的两个极值点,其中
的两个极值点,其中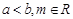 .
.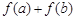 的取值范围;
的取值范围;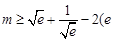 为自然对数的底数),求
为自然对数的底数),求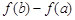 的最大值.
的最大值.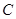 :
: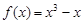
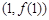 处的切线方程;
处的切线方程;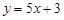 平行的曲线C的切线方程.
平行的曲线C的切线方程.
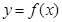 的单调区间;
的单调区间;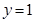 恰有两个交点,求
恰有两个交点,求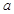 的取值范围.
的取值范围.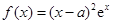 在
在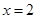 时取得极小值.
时取得极小值. 的值;
的值;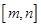 ,使得
,使得 在该区间上的值域为
在该区间上的值域为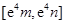 ?若存在,求出
?若存在,求出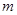 ,
,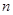 的值;
的值;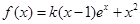 .
. ,求函数
,求函数 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;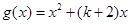 的图象恒在
的图象恒在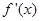 图象的上方,求k的取值范围;
图象的上方,求k的取值范围;