题目内容
【题目】设函数f(x)=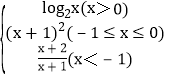 ,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先画出函数f(x)图像,记t=f(x0),存在唯一的x0,所以必有t>1,所以f(t)=2a2m2+am>1对任意给定的m∈(1,+∞)恒成立,因式分解得(ma+1)(2ma-1)>0,因为ma+1>0,所以2ma-1>0恒成立,代入m=1即可.
解:作出函数f(x)的图象如图:由图象知当x>0时,f(x)=log2x的值域为R,
当-1≤x≤0,f(x)的取值范围为[0,1],
当x<-1时,f(x)的取值范围是(-∞,1),
即由图象知当f(x)≤1时,x的值不唯一,设t=f(x0),
当x>0时,由f(x)=log2x≥1得x≥2,则方程f(f(x0))=2a2m2+am,
等价为f(t)=2a2m2+am,
因为2a2m2+am>0
所以若存在唯一的x0∈R满足f(f(x0))=2a2m2+am,
则t>1,即由f(x)=log2x>1得x>2,
即当x>2时,f(f(x))与x存在一一对应的关系,则此时必有f(f(x))>1,
即2a2m2+am>1,得(ma+1)(2ma-1)>0,
因为ma+1>0,
所以不等式等价为2ma-1>0,设h(m)=2ma-1,
因为m>1,a>0,
所以只要h(1)≥0即可,得2a-1≥0,得a≥![]() ,
,
即实数a的取值范围是[![]() ,+∞).
,+∞).
故选:A.
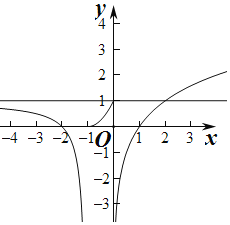

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
