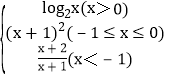题目内容
【题目】已知数列{an}为等差数列，a1=3且（a3﹣1）是（a2﹣1）与a4的等比中项．
（1）求an；
（2）若数列{an}的前n项和为Sn ， bn= 
，Tn=﹣b1+b2+b3+…+（﹣1）nbn ， 求Tn ．
【答案】
（1）解：设等差数列{an}的公差为d，a1=3且（a3﹣1）是（a2﹣1）与a4的等比中项．
∴（3+2d﹣1）2=（3+3d）（3+d﹣1），整理为：d2﹣d﹣2=0，解得d=2，或﹣1（舍去）．
∴an=2n+1．
（2）解：Sn= 
=n2+2n
bn= 
= 
= 
，
当n为偶数时，Tn=﹣b1+b2+b3+…+（﹣1）nbn=﹣ 
+ 
﹣…+ 
=﹣1+ 
= 
．
当n为奇数时，Tn=﹣b1+b2+b3+…+（﹣1）nbn=﹣ + ﹣…﹣ =﹣1﹣ = 
．
∴Tn=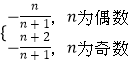 
【解析】（1）设等差数列{an}的公差为d，a1=3且（a3﹣1）是（a2﹣1）与a4的等比中项．可得（3+2d﹣1）2=（3+3d）（3+d﹣1），整理为：d2﹣d﹣2=0，解得d并且验证即可得出．（2）Sn= =n2+2n，bn= = = ，对n分类讨论即可得出．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系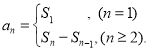
．
【题目】2017年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：
上春晚次数x（单位：次） | 2 | 4 | 6 | 8 | 10 |
粉丝数量y（单位：万人） | 10 | 20 | 40 | 80 | 100 |
（1）若该演员的粉丝数量g（x）≤g（1）=0与上春晚次数x满足线性回归方程，试求回归方程 
= 
x+ 
，并就此分析，该演员上春晚12次时的粉丝数量；
（2）若用 
（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望． 参考公式： = 
， = 
﹣ 
．
