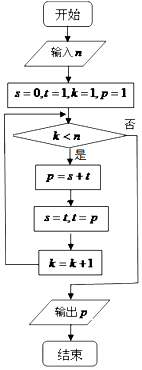
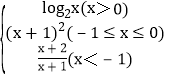题目内容
【题目】若集合A={x|2 
＞1}，集合B={x|y=lg 
}，则A∩B=（ ）
A.{x|﹣5＜x＜1}
B.{x|﹣2＜x＜1}
C.{x|﹣2＜x＜﹣1}
D.{x|﹣5＜x＜﹣1}
【答案】C
【解析】解：由2 
＞1=20 ， 得到x2﹣4x﹣5＞0，解得x＜﹣1，或x＞5， ∴集合A={x|x＜﹣1，或x＞5}，
由集合B={x|y=lg 
}，得到 ＞0，即（x+2）（x﹣2）＜0，解得﹣2＜x＜2，
∴集合B={x|﹣2＜x＜2}，
∴A∩B={x|﹣2＜x＜﹣1}，
故选：C．
【考点精析】本题主要考查了集合的交集运算的相关知识点，需要掌握交集的性质：（1）A∩B
A，A∩BB，A∩A=A，A∩
=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】2017年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：
上春晚次数x（单位：次） | 2 | 4 | 6 | 8 | 10 |
粉丝数量y（单位：万人） | 10 | 20 | 40 | 80 | 100 |
（1）若该演员的粉丝数量g（x）≤g（1）=0与上春晚次数x满足线性回归方程，试求回归方程 
= 
x+ 
，并就此分析，该演员上春晚12次时的粉丝数量；
（2）若用 
（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望． 参考公式： = 
， = 
﹣ 
．
