题目内容
已知椭圆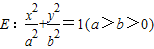 的左、右焦点为F1,F2,且离心率为
的左、右焦点为F1,F2,且离心率为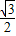 .
.(1)若过F1的直线交椭圆E于P,Q两点,且
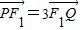 ,求直线PQ的斜率;
,求直线PQ的斜率;(2)若椭圆E过点(0,1),且过F1作两条互相垂直的直线,它们分别交椭圆E于A,C和B,D,求四边形ABCD面积的最大值和最小值.
【答案】分析:(1)利用椭圆的第二定义,构建三角形,求得三边长,即可求得直线PQ的斜率;
(2)求出椭圆方程,当AC为2a,DB⊥x轴时,面积有最大值,最大值为2;当两条直线斜率都存在时,求出AC,BD的长,表示出四边形ABCD面积为S= |AC||BD|,利用基本不等式,即可求得结论.
|AC||BD|,利用基本不等式,即可求得结论.
解答:解:(1)设椭圆的左准线为l,作PD⊥x轴于D,作PN⊥l于N,由第二定义得|PN|=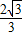 |PF1|.
|PF1|.
作QM⊥l于M,得|QM|=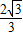 |F1Q|=
|F1Q|= |PF1|,
|PF1|,
作QE⊥PN于E,交轴于点A得|EP|=4|AF1|=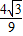 |PF1|,
|PF1|,
∴|F1D|=3|AF1|= |PF1|,
|PF1|,
∴|PD|=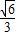 |PF1|,
|PF1|,
∴直线PQ的斜率为±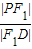 =
=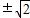 ;
;
(2)由题意,b=1,又 ,∴a=2,b=1,c=
,∴a=2,b=1,c=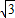 ,
,
∴椭圆方程为 .
.
∵DB、AC为过焦点的两条直线,∴当AC为2a,DB⊥x轴时,面积有最大值,最大值为2;
当两条直线斜率都存在时,F1(-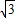 ,0),设直线AC的方程为y=k(x-
,0),设直线AC的方程为y=k(x-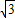 )
)
与椭圆联立消去y,(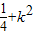 )x2-
)x2-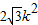 x+3k2-1=0
x+3k2-1=0
设A(x1,y1),C(x2,y2),则x1+x2= ,x1x2=
,x1x2=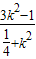
∴|AC|=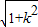 |x1-x2|=
|x1-x2|=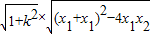 =
=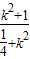
同理可得|BD|= ,
,
∴四边形ABCD面积为S= |AC||BD|=
|AC||BD|= ×
×
令t=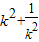 ,则t≥2,∴S=
,则t≥2,∴S= ×
×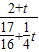 =2×
=2×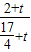 =2(1-
=2(1-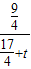 )
)
∵t≥2,∴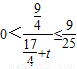 ,∴
,∴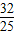 ≤S<2
≤S<2
∴四边形ABCD面积最小值为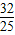 .
.
点评:本题考查椭圆的第二定义,考查直线与椭圆的位置关系,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.
(2)求出椭圆方程,当AC为2a,DB⊥x轴时,面积有最大值,最大值为2;当两条直线斜率都存在时,求出AC,BD的长,表示出四边形ABCD面积为S=
 |AC||BD|,利用基本不等式,即可求得结论.
|AC||BD|,利用基本不等式,即可求得结论.解答:解:(1)设椭圆的左准线为l,作PD⊥x轴于D,作PN⊥l于N,由第二定义得|PN|=
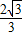 |PF1|.
|PF1|.作QM⊥l于M,得|QM|=
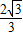 |F1Q|=
|F1Q|= |PF1|,
|PF1|,作QE⊥PN于E,交轴于点A得|EP|=4|AF1|=
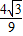 |PF1|,
|PF1|,∴|F1D|=3|AF1|=
 |PF1|,
|PF1|,∴|PD|=
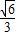 |PF1|,
|PF1|,∴直线PQ的斜率为±
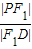 =
=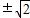 ;
;(2)由题意,b=1,又
 ,∴a=2,b=1,c=
,∴a=2,b=1,c=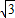 ,
,∴椭圆方程为
 .
.∵DB、AC为过焦点的两条直线,∴当AC为2a,DB⊥x轴时,面积有最大值,最大值为2;
当两条直线斜率都存在时,F1(-
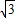 ,0),设直线AC的方程为y=k(x-
,0),设直线AC的方程为y=k(x-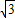 )
)与椭圆联立消去y,(
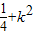 )x2-
)x2-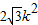 x+3k2-1=0
x+3k2-1=0设A(x1,y1),C(x2,y2),则x1+x2=
 ,x1x2=
,x1x2=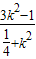
∴|AC|=
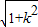 |x1-x2|=
|x1-x2|=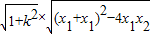 =
=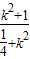
同理可得|BD|=
 ,
,∴四边形ABCD面积为S=
 |AC||BD|=
|AC||BD|= ×
×
令t=
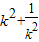 ,则t≥2,∴S=
,则t≥2,∴S= ×
×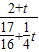 =2×
=2×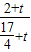 =2(1-
=2(1-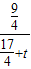 )
)∵t≥2,∴
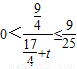 ,∴
,∴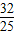 ≤S<2
≤S<2∴四边形ABCD面积最小值为
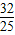 .
.点评:本题考查椭圆的第二定义,考查直线与椭圆的位置关系,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线