题目内容
已知命题 “存在
“存在 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在 轴上的椭圆”,命题
轴上的椭圆”,命题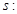 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
(1)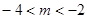 或
或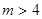 ;(2)
;(2)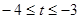 或
或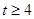
解析试题分析:(1)依题意说明命题 和命题
和命题 都是真命题。命题
都是真命题。命题 为真,因二次函数图像开口向上,则判别式应大于等于0;命题
为真,因二次函数图像开口向上,则判别式应大于等于0;命题 为真,则两分母均大于0,且
为真,则两分母均大于0,且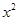 下的分母较大。(2)命题
下的分母较大。(2)命题 是真命题,则两分母异号,因
是真命题,则两分母异号,因 是
是 的必要不充分条件,命题
的必要不充分条件,命题 解集是命题
解集是命题 解集的真子集。
解集的真子集。
试题解析:解:(1)若 为真:
为真: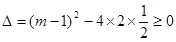 1分
1分
解得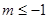 或
或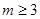 2分
2分
若 为真:则
为真:则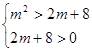 3分
3分
解得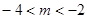 或
或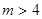 4分
4分
若“ 且
且 ”是真命题,则
”是真命题,则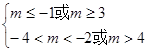 6分
6分
解得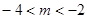 或
或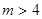 7分
7分
(2)若 为真,则
为真,则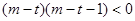 ,即
,即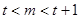 8分
8分
由 是
是 的必要不充分条件,
的必要不充分条件,
则可得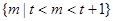
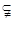
 或
或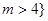 9分
9分
即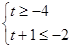 或
或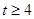 11分
11分
解得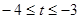 或
或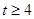 12分
12分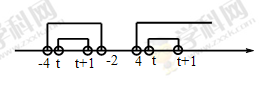
考点:1命题的真假判断;2充分必要条件。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
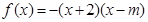 (其中
(其中 ).
).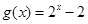 .
.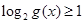 ”是假命题,求
”是假命题,求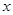 的取值范围;
的取值范围; :
: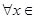
 ,
,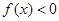 或
或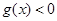 ;命题
;命题 :
: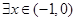 ,
,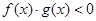 .若
.若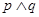 是真命题,求
是真命题,求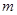 的取值范围.
的取值范围. :
: ,命题
,命题 :
: ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. 方程
方程 在
在 上有解;命题
上有解;命题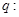 不等式
不等式 恒成立,若命题“
恒成立,若命题“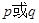 ”是假命题,求
”是假命题,求 的取值范围.
的取值范围. ,命题q:
,命题q: ,若
,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围. :方程
:方程 表示焦点在
表示焦点在 轴的椭圆;命题
轴的椭圆;命题 :关于
:关于 的不等式
的不等式 的解集是R;若“
的解集是R;若“ ” 是假命题,“
” 是假命题,“ ”是真命题,求实数
”是真命题,求实数 的取值范围。
的取值范围。 ,设
,设 :函数
:函数 在
在 上单调递减,
上单调递减, :曲线
:曲线 与
与 轴交于不同的两点。若“
轴交于不同的两点。若“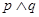 ”为假命题,“
”为假命题,“ ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。