题目内容
已知 ,设
,设 :函数
:函数 在
在 上单调递减,
上单调递减, :曲线
:曲线 与
与 轴交于不同的两点。若“
轴交于不同的两点。若“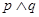 ”为假命题,“
”为假命题,“ ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
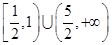 .
.
解析试题分析:先就命题 和命题
和命题 均为真命题时求参数
均为真命题时求参数 的取值范围,然后根据题中条件确定命题
的取值范围,然后根据题中条件确定命题 和命题
和命题 的真假性,若有多种情况,应对两个命题的真假性进行分类讨论,并确定各种情况下参数
的真假性,若有多种情况,应对两个命题的真假性进行分类讨论,并确定各种情况下参数 的取值范围,最后再将各情况下
的取值范围,最后再将各情况下 的取值范围取并集即可得到
的取值范围取并集即可得到 的取值范围.
的取值范围.
试题解析:当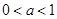 时,函数
时,函数 在
在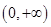 内单调递减,
内单调递减,
当 时,函数
时,函数 在
在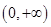 内不是单调递减。 2分
内不是单调递减。 2分
曲线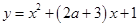 与
与 轴有两个不同的交点等价于
轴有两个不同的交点等价于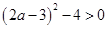 ,
,
即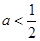 或
或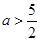 。 4分
。 4分
①若 正确,且
正确,且 不正确,则
不正确,则 ,即
,即 ; 6分
; 6分
②若 不正确,且
不正确,且 正确,则
正确,则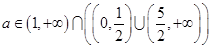 ,即
,即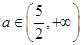 。 8分
。 8分
综上, 的取值范围为
的取值范围为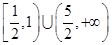 。 9分
。 9分
考点:函数的单调性、二次函数零点个数的判断、复合命题

练习册系列答案
相关题目
 “存在
“存在 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在 轴上的椭圆”,命题
轴上的椭圆”,命题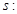 “曲线
“曲线 表示双曲线”
表示双曲线” 且
且 的取值范围;
的取值范围; 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。 :不等式
:不等式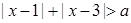 对一切实数
对一切实数 都成立;命题
都成立;命题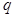 :已知函数
:已知函数 的图像在点
的图像在点 处的切线恰好与直线
处的切线恰好与直线 平行,且
平行,且 在
在 上单调递减。若命题
上单调递减。若命题 的取值范围。
的取值范围。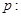 方程
方程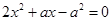 在[-1,1]上有解;命题
在[-1,1]上有解;命题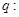 只有一个实数
只有一个实数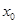 满足不等式
满足不等式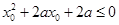 ,若命题“p∨q”是假命题,求实数
,若命题“p∨q”是假命题,求实数 的取值范围.
的取值范围.
 ;命题
;命题
 ,若
,若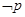 是
是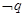 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.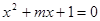 有两个不等的负实根,命题q:方程
有两个不等的负实根,命题q:方程
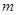 的取值范围.
的取值范围. ,
, .
.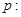 函数
函数 是增函数.命题
是增函数.命题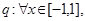
 成立,若
成立,若 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. 实数x满足
实数x满足 (其中
(其中 ),命题
),命题 实数
实数 满足
满足
 ,且
,且 为真,求实数
为真,求实数 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.