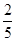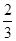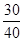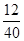题目内容
.已知f(x),g(x)都是定义在R上的函数,f(x)=ax×g(x),(a>0且a¹1),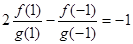 ,在有穷数列{
,在有穷数列{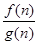 }(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{
}(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{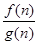 }前k项和大于
}前k项和大于 的概率是( )
的概率是( )
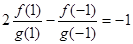 ,在有穷数列{
,在有穷数列{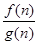 }(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{
}(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{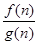 }前k项和大于
}前k项和大于 的概率是( )
的概率是( )A. | B. | C. | D. |
C
解:因为由已知可知f(x)=ax×g(x),即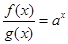 ,根据已知条件
,根据已知条件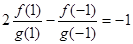 求解a=
求解a=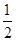 ,然后得到
,然后得到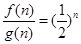 ,任取正整数k(1£k£10),则数列{
,任取正整数k(1£k£10),则数列{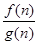 }前k项和大于
}前k项和大于 ,即为等比数列的前k项和大于
,即为等比数列的前k项和大于 ,得到k的值,从而∴k>4,又因为k为正整数,k=5,6,7,8,9,10共6种结果,而所有偶的情况为10种,因此概率值为
,得到k的值,从而∴k>4,又因为k为正整数,k=5,6,7,8,9,10共6种结果,而所有偶的情况为10种,因此概率值为 ,选C
,选C
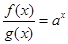 ,根据已知条件
,根据已知条件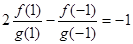 求解a=
求解a=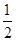 ,然后得到
,然后得到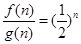 ,任取正整数k(1£k£10),则数列{
,任取正整数k(1£k£10),则数列{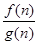 }前k项和大于
}前k项和大于 ,即为等比数列的前k项和大于
,即为等比数列的前k项和大于 ,得到k的值,从而∴k>4,又因为k为正整数,k=5,6,7,8,9,10共6种结果,而所有偶的情况为10种,因此概率值为
,得到k的值,从而∴k>4,又因为k为正整数,k=5,6,7,8,9,10共6种结果,而所有偶的情况为10种,因此概率值为 ,选C
,选C
练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 .
. ,
, )
)



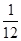
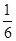
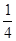
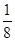




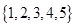 中任取一个偶数
中任取一个偶数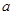 和一个奇数
和一个奇数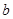 构成以原点为起点的向量
构成以原点为起点的向量 .从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为
.从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为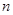 ,其中面积不超过
,其中面积不超过 的平行四边形的个数为
的平行四边形的个数为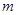 ,则
,则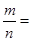 ( )
( )