题目内容
定义在R上的可导函数f(x),已知y=e f ′(x)的图象如下图所示,则y=f(x)的增区间是
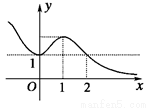
A.(-∞,1) B.(-∞,2) C.(0,1) D.(1,2)
【答案】
B
【解析】
试题分析:若f‘(x)≥0,则e f ′(x)≥ e0=1,由图知当x<2时,e f ′(x)≥ 1,所以y=f(x)的增区间是(-∞,2) 。
考点:指数函数的图像;指数函数的性质;利用导数研究函数的单调性。
点评:要求函数y=f(x)的增区间,只需求f‘(x)>0的解集。因此根据y=e f ′(x)的图像判断f‘(x)>0的解集时解题的关键。属于中档题。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
定义在R上的可导函数y=f(x)在x=1处的切线方程是y=-x+2,则f(1)+f'(1)=( )
| A、-1 | ||
B、
| ||
| C、2 | ||
| D、0 |
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x2+2xf′(2),则f(-
)与f(
)的大小关系是( )
| 1 |
| 2 |
| 16 |
| 3 |
A、f(-
| ||||
B、f(-
| ||||
C、f(-
| ||||
| D、不确定 |