题目内容
9.设函数f(x)=ax-bx2(a>0).(1)当b>1时,若对任意x∈[0,1],都有|f(x)|≤1,证明:b-1≤a≤2$\sqrt{b}$;
(2)当0<b≤1时,若对任意x[0,1],都有|f(x)|≤1,求a的取值范围.
分析 (1)讨论绝对值不等式|f(x)|≤1的解集为f(x)≤1或f(x)≥-1,分别得到a的范围,求出公共解集即可,
(2)由f(x)≤1得到a-b≤1即a≤b+1,继而得到a的范围.
解答 证明:对任意x∈[0,1],|f(x)|≤1⇒f(x)≥-1.
据此可推出f(1)≥-1,即a-b≥-1,
∴a≥b-1.
对任意x∈[0,1],|f(x)|≤1⇒f(x)≤1,
因为b>1,可得0<$\frac{1}{\sqrt{b}}$<1,可推出f($\frac{1}{\sqrt{b}}$)≤1,即a•$\frac{1}{\sqrt{b}}$-1≤1,
∴a≤2$\sqrt{b}$,
∴b-1≤a≤2$\sqrt{b}$.
(3)解:因为a>0,0<b≤1时,对任意x∈[0,1]有f(x)=ax-bx2≥-b≥-1,即f(x)≥-1;
f(x)≤1⇒f(1)≤1⇒a-b≤1,
即a≤b+1.
故a的取值范围为(0,b+1)
点评 本题考查了绝对值不等式的证明和参数的取值范围,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
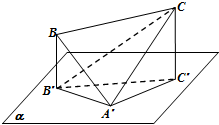 如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.