题目内容
曲线C1的极坐标方程为:ρ=2sinθ,曲线C2的参数方程为:
(t为参数),则C1和C2所表示的图形分别是 ( )
|
分析:先将原极坐标方程两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断C1所表示的图形;将C2的参数方程消去参数后化成直角坐标方程即可得到结论.
解答:解:∵ρ=2sinθ
∴ρ2=4ρsinθ
∴x2+y2=4y
∴C1的直角坐标方程为x2+y2-4y=0
∴C1所表示的图形是圆(4分)
∵曲线C2的参数方程为:
(t为参数),
消去参数t得:3x+4y-11=0.
∴C2所表示的图形是直线.
故选:A.
∴ρ2=4ρsinθ
∴x2+y2=4y
∴C1的直角坐标方程为x2+y2-4y=0
∴C1所表示的图形是圆(4分)
∵曲线C2的参数方程为:
|
消去参数t得:3x+4y-11=0.
∴C2所表示的图形是直线.
故选:A.
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
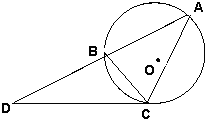 (1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,
(1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,