题目内容
本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分
(1)选修4-2:矩阵与变换
变换T是将平面上每个点M(x,y)的横坐标乘2,纵坐标乘4,变到点M′(2x,4y).
(Ⅰ)求变换T的矩阵;
(Ⅱ)圆C:x2+y2=1在变换T的作用下变成了什么图形?
(2)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线C1的极坐标方程为:5ρ2-3ρ2cos2θ-8=0,直线?的参数方程为:
(t为参数).
(Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)直线?上有一定点P(1,0),曲线C1与?交于M,N两点,求|PM|.|PN|的值.
(3)选修4-5:不等式选讲
已知a,b,c为实数,且a+b+c+2-2m=0,a2+
b2+
c2+m-1=0.
(Ⅰ)求证:a2+
b2+
c2≥
;
(Ⅱ)求实数m的取值范围.
(1)选修4-2:矩阵与变换
变换T是将平面上每个点M(x,y)的横坐标乘2,纵坐标乘4,变到点M′(2x,4y).
(Ⅰ)求变换T的矩阵;
(Ⅱ)圆C:x2+y2=1在变换T的作用下变成了什么图形?
(2)选修4-4:坐标系与参数方程
已知极点与原点重合,极轴与x轴的正半轴重合.若曲线C1的极坐标方程为:5ρ2-3ρ2cos2θ-8=0,直线?的参数方程为:
|
(Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)直线?上有一定点P(1,0),曲线C1与?交于M,N两点,求|PM|.|PN|的值.
(3)选修4-5:不等式选讲
已知a,b,c为实数,且a+b+c+2-2m=0,a2+
| 1 |
| 4 |
| 1 |
| 9 |
(Ⅰ)求证:a2+
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
(Ⅱ)求实数m的取值范围.
分析:(1)(Ⅰ)由题意可得T:
→
=
=
,
,由此得到变换T的矩阵.
(Ⅱ)由 x′=2x,y′=4y,代入方程 x2+y2=1,得:
x′2+
y′2=1,由此得出结论.
(2)(Ⅰ)在曲线C1的极坐标方程中,把极坐标和直角坐标的互化公式代入,化简整理得到曲线C1的直角坐标方程.
(Ⅱ)把直线的参数方程代入到曲线C1的直角坐标方程,得7t2-2
t-3=0,t1t2=-
,由t的几何意义求得
|PM|•|PN|的值.
(3)(Ⅰ)由柯西不等式得 [a2+(
b)2+(
c)2] • [12+22+32]≥(a+b+c)2,两边同时除以14,即可证得
结论.
(Ⅱ)由已知得 14(1-m)≥(2m-2)2,解一元二次不等式求得实数m的取值范围.再由
a2+
b2+
c2=1-m≥0,可得m≤1.把这两个实数m的取值范围取交集,即得所求.
|
|
|
|
|
|
(Ⅱ)由 x′=2x,y′=4y,代入方程 x2+y2=1,得:
| 1 |
| 4 |
| 1 |
| 16 |
(2)(Ⅰ)在曲线C1的极坐标方程中,把极坐标和直角坐标的互化公式代入,化简整理得到曲线C1的直角坐标方程.
(Ⅱ)把直线的参数方程代入到曲线C1的直角坐标方程,得7t2-2
| 3 |
| 3 |
| 7 |
|PM|•|PN|的值.
(3)(Ⅰ)由柯西不等式得 [a2+(
| 1 |
| 2 |
| 1 |
| 3 |
结论.
(Ⅱ)由已知得 14(1-m)≥(2m-2)2,解一元二次不等式求得实数m的取值范围.再由
a2+
| 1 |
| 4 |
| 1 |
| 9 |
解答:(1)解:(Ⅰ)由已知得T:
→
=
=
,
,
∴变换T的矩阵是
,
…(3分)
(Ⅱ)由 x′=2x,y′=4y,得:x=
x′,y=
y′,…(4分)
代入方程 x2+y2=1,得:
x′2+
y′2=1. …(6分)
∴圆C:x2+y2=1在变化T的作用下变成了椭圆
+
=1…(7分)
(2)解:(Ⅰ)由5ρ2-3ρ2cos2θ-8=0得,5ρ2-3ρ2(cos2θ-sin2θ)-8=0,
即5ρ2-3ρ2cos2θ+3ρ2sin2θ-8=0,从而5(x2+y2)-3x2+3y2-8=0,
整理得
+y2=1.…(3分)
(Ⅱ)把直线的参数方程代入到曲线C1的直角坐标方程,得7t2-2
t-3=0,t1t2=-
.
由t的几何意义知|PM|.|PN|=|t1•t2|=
.…(7分)
(3)解:(Ⅰ)由柯西不等式得 [a2+(
b)2+(
c)2] • [12+22+32]≥(a+b+c)2,…(2分)
即(a2+
b2+
c2)×14≥(a+b+c)2,∴a2+
b2+
c2≥
. …(4分)
(Ⅱ)由已知得a+b+c=2m-2,a2+
b2+
c2=1-m,
∴14(1-m)≥(2m-2)2,即 2m2+3m-5≤0,∴-
≤m≤1.…(6分)
又∵a2+
b2+
c2=1-m≥0,∴m≤1,∴-
≤m≤1.…(7分)
|
|
|
|
|
|
∴变换T的矩阵是
|
|
(Ⅱ)由 x′=2x,y′=4y,得:x=
| 1 |
| 2 |
| 1 |
| 4 |
代入方程 x2+y2=1,得:
| 1 |
| 4 |
| 1 |
| 16 |
∴圆C:x2+y2=1在变化T的作用下变成了椭圆
| x2 |
| 4 |
| y2 |
| 16 |
(2)解:(Ⅰ)由5ρ2-3ρ2cos2θ-8=0得,5ρ2-3ρ2(cos2θ-sin2θ)-8=0,
即5ρ2-3ρ2cos2θ+3ρ2sin2θ-8=0,从而5(x2+y2)-3x2+3y2-8=0,
整理得
| x2 |
| 4 |
(Ⅱ)把直线的参数方程代入到曲线C1的直角坐标方程,得7t2-2
| 3 |
| 3 |
| 7 |
由t的几何意义知|PM|.|PN|=|t1•t2|=
| 3 |
| 7 |
(3)解:(Ⅰ)由柯西不等式得 [a2+(
| 1 |
| 2 |
| 1 |
| 3 |
即(a2+
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
(Ⅱ)由已知得a+b+c=2m-2,a2+
| 1 |
| 4 |
| 1 |
| 9 |
∴14(1-m)≥(2m-2)2,即 2m2+3m-5≤0,∴-
| 5 |
| 2 |
又∵a2+
| 1 |
| 4 |
| 1 |
| 9 |
| 5 |
| 2 |
点评:本题主要考查 几种矩阵运算、直线的参数方程、柯西不等式的应用,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
. 在变换
在变换 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数). ,曲线
,曲线 的值.
的值. 为实数,且
为实数,且

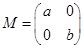 (其中a>0,b>0).
(其中a>0,b>0).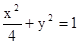 ,求a,b的值.
,求a,b的值. (其中a>0,b>0).
(其中a>0,b>0).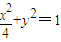 ,求a,b的值.
,求a,b的值. .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;