题目内容
【题目】如图,中心为坐标原点O的两圆半径分别为![]() ,
,![]() ,射线OT与两圆分别交于A、B两点,分别过A、B作垂直于x轴、y轴的直线
,射线OT与两圆分别交于A、B两点,分别过A、B作垂直于x轴、y轴的直线![]() 、
、![]() ,
,![]() 交
交![]() 于点P.
于点P.
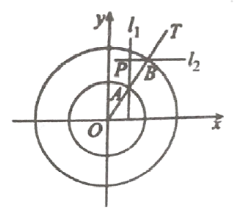
(1)当射线OT绕点O旋转时,求P点的轨迹E的方程;
(2)直线l:![]() 与曲线E交于M、N两点,两圆上共有6个点到直线l的距离为
与曲线E交于M、N两点,两圆上共有6个点到直线l的距离为![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1) 设![]() ,OT与x轴正方向夹角为
,OT与x轴正方向夹角为![]() ,写出
,写出![]() 轨迹的参数方程,再化简成直角坐标方程即可.
轨迹的参数方程,再化简成直角坐标方程即可.
(2)根据两圆上共有6个点到直线l的距离为![]() ,利用圆的位置关系转换为原点O至直线l的距离
,利用圆的位置关系转换为原点O至直线l的距离![]() ,进而求得
,进而求得![]() 的取值范围,再联立直线与椭圆表达出
的取值范围,再联立直线与椭圆表达出![]() ,利用
,利用![]() 的取值范围求解
的取值范围求解![]() 的取值范围即可.
的取值范围即可.
设![]() ,OT与x轴正方向夹角为
,OT与x轴正方向夹角为![]() ,则
,则
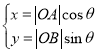 即
即![]()
化简得![]() ,即P点的轨迹E的方程为
,即P点的轨迹E的方程为![]()
(2)当两圆上有6个点到直线1的距离为![]() 时,原点O至直线l的距离
时,原点O至直线l的距离![]() ,
,
即 ,解得
,解得![]()
联立方程 得
得![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
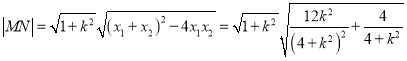

则![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目