题目内容
【题目】若数列
前
项和为
(1)若首项
,且对于任意的正整数
均有
,(其中
为正实常数),试求出数列的通项公式.
(2)若数列是等比数列,公比为
,首项为
,为给定的正实数,满足:①
,且
②对任意的正整数,均有
;试求函数
的最大值(用和表示)
【答案】(1)
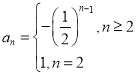(2)
【解析】
(1)先根据
,(其中
为正实常数),求出
,然后利用
进行求解,注意验证首项;
(2)先求出
,然后根据条件判定
的符号,从而确定
的单调性,从而求出最大值.
解:(1)∵,(其中为正实常数),
∴，所以当
时，
，因为
，所以
∴当
时
，即
,
所以数列
从第二项起，是以
为公比的等比数列，所以
时，
，
∴
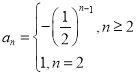
(2)由题意，因为
所以
∵
,且
对任意的正整数
,均有
，
∴
，
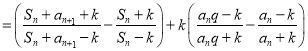
因为
，由题中条件可得：
，
，
，，
，
，
，
所以
，
，
即
，
∴是一个关于的单调递减的函数,最大值为
.
练习册系列答案
阅读快车系列答案
相关题目
