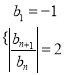题目内容
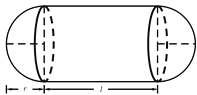
【题目】某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,![]() (
(![]() 为圆柱的高,为球的半径,
为圆柱的高,为球的半径,![]() ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为![]() 千元,半球形部分每平方米建造费用为
千元,半球形部分每平方米建造费用为![]() 千元.设该储油罐的建造费用为
千元.设该储油罐的建造费用为![]() 千元.
千元.
(1) 写出![]() 关于
关于![]() 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2) 若预算为![]() 万元,求所能建造的储油罐中
万元,求所能建造的储油罐中![]() 的最大值(精确到
的最大值(精确到![]() ),并求此时储油罐的体积
),并求此时储油罐的体积![]() (单位: 立方米,精确到
(单位: 立方米,精确到![]() 立方米).
立方米).
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() (米),
(米),![]() 立方米.
立方米.
【解析】
(1)先利用公式计算两个半球的表面积(不含底)以及圆柱的侧面积,再根据每平方米建造费用可得![]() 关于
关于![]() 的函数表达式,注意
的函数表达式,注意![]() 的范围.
的范围.
(2)根据预算可得关于![]() 的不等式,求出其解后可得
的不等式,求出其解后可得![]() 的最大值,利用公式可求该几何体的体积.
的最大值,利用公式可求该几何体的体积.
(1) 半球的表面积![]() (不含底),圆柱的侧面积
(不含底),圆柱的侧面积![]() .
.
于是![]() .
.
定义域为![]() .
.
(2) ![]() ,即
,即![]() ,解得
,解得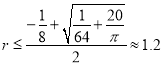 .
.
![]() ,
,
经计算得![]() (立方米).
(立方米).
故![]() 的最大值为
的最大值为![]() (米),此时储油罐的体积约为
(米),此时储油罐的体积约为![]() 立方米.
立方米.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目