题目内容
【题目】已知函数![]() 是关于
是关于![]() 的偶函数.
的偶函数.
(1)求![]() 的值;
的值;
(2)求证: 对任意实数![]() ,函数
,函数![]() 的图象与函数
的图象与函数![]() 的图象最多只有一个交点.
的图象最多只有一个交点.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)通过函数![]() 是关于
是关于![]() 的偶函数,可得
的偶函数,可得![]() 恒成立,可得
恒成立,可得
![]() 恒成立,从而可求
恒成立,从而可求![]() 的值;(2) 由
的值;(2) 由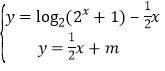 , 得
, 得![]() , 所以
, 所以![]() ,令
,令![]() ,利用单调性的定义可证明
,利用单调性的定义可证明![]() 在
在![]() 上单调递减,从而可得结论.
上单调递减,从而可得结论.
(1)因为f(x)是关于x的偶函数,
所以log2(2 - x + 1) + k( - x) = log2(2x + 1) + kx, 即2kx = log2![]() = - x, 解得k = -
= - x, 解得k = -![]() .
.
(2) 由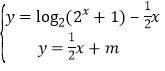 , 得log2(2x + 1) -
, 得log2(2x + 1) -![]() x =
x =![]() x + m,
x + m,
所以 m = log2(2x + 1) -x = log2(1 +![]() ). 令h(x) = log2(1 +
). 令h(x) = log2(1 +![]() ),
),
设x1, x2 R, 且x1 < x2, 则![]() >
>![]() , 所以log2(1 +
, 所以log2(1 +![]() ) > log2(1 +
) > log2(1 +![]() ),
),
所以h(x1) – h(x2) = log2(1 +![]() ) - log2(1 +
) - log2(1 +![]() ) > 0, 即 h(x1) > h(x2), ∴ h(x)在R上单调递减.
) > 0, 即 h(x1) > h(x2), ∴ h(x)在R上单调递减.
因此, 函数y = h(x)的图象与直线y = m的图象最多只有一个交点. 所以, 对任意实数m, 函数y = f(x)的图象与直线y =![]() x + m的图象最多只有一个交点.
x + m的图象最多只有一个交点.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目



