题目内容
【题目】甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束.经抽签，甲、乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为
，
（1）求甲连胜四场的概率；
（2）求需要进行第五场比赛的概率；
（3）求丙最终获胜的概率.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率；
（2）计算出四局以内结束比赛的概率，然后利用对立事件的概率公式可求得所求事件的概率；
（3）列举出甲赢的基本事件，结合独立事件的概率乘法公式计算出甲赢的概率，由对称性可知乙赢的概率和甲赢的概率相等，再利用对立事件的概率可求得丙赢的概率.
（1）记事件
甲连胜四场，则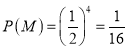
；
（2）记事件
为甲输，事件
为乙输，事件
为丙输，
则四局内结束比赛的概率为
，
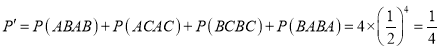所以，需要进行第五场比赛的概率为
；
（3）记事件为甲输，事件为乙输，事件为丙输，
记事件甲赢，记事件
丙赢，
则甲赢的基本事件包括：
、
、
、
、
、
、
、
，
所以，甲赢的概率为
.
由对称性可知，乙赢的概率和甲赢的概率相等，
所以丙赢的概率为
.
【题目】某厂接受了一项加工业务，加工出来的产品(单位：件)按标准分为A，B，C，D四个等级.加工业务约定：对于A级品、B级品、C级品，厂家每件分别收取加工费90元，50元，20元；对于D级品，厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：
甲分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 40 | 20 | 20 | 20 |
乙分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 28 | 17 | 34 | 21 |
（1）分别估计甲、乙两分厂加工出来的一件产品为A级品的概率；
（2）分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务?
【题目】（理）某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在
内，发布成绩使用等级制各等级划分标准见下表，规定：
三级为合格等级，
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况，从中抽取了
名学生的原始成绩作为样本进行统计，按照
的分组作出频率分布直方图如图所示，样本中分数在80分及以上的所有数据的茎叶图如图所示.，
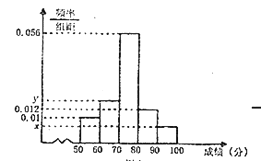
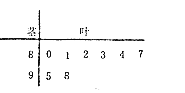
（1）求和频率分布直方图中的
的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选3人，求至少有1人成绩是合格等级的概率；
（3）在选取的样本中，从
两个等级的学生中随机抽取了3名学生进行调研，记
表示所抽取的
名学生中为
等级的学生人数，求随机变量的分布列及数学期望.
