题目内容
【题目】已知椭圆C1:![]() (a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=
(a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=![]() |AB|.
|AB|.
(1)求C1的离心率;
(2)设M是C1与C2的公共点,若|MF|=5,求C1与C2的标准方程.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)求出![]() 、
、![]() ,利用
,利用![]() 可得出关于
可得出关于![]() 、
、![]() 的齐次等式,可解得椭圆
的齐次等式,可解得椭圆![]() 的离心率的值;
的离心率的值;
(2)由(1)可得出![]() 的方程为
的方程为![]() ,联立曲线
,联立曲线![]() 与
与![]() 的方程,求出点
的方程,求出点![]() 的坐标,利用抛物线的定义结合
的坐标,利用抛物线的定义结合![]() 可求得
可求得![]() 的值,进而可得出
的值,进而可得出![]() 与
与![]() 的标准方程.
的标准方程.
(1)![]() ,
,![]() 轴且与椭圆
轴且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,
则直线![]() 的方程为
的方程为![]() ,
,
联立 ,解得
,解得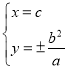 ,则
,则![]() ,
,

抛物线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,
,
解得![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
即![]() ,即
,即![]() ,
,
![]() ,解得
,解得![]() ,因此,椭圆
,因此,椭圆![]() 的离心率为
的离心率为![]() ;
;
(2)由(1)知![]() ,
,![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() ,
,
联立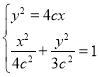 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
由抛物线的定义可得![]() ,解得
,解得![]() .
.
因此,曲线![]() 的标准方程为
的标准方程为![]() ,
,
曲线![]() 的标准方程为
的标准方程为![]() .
.

【题目】十九大报告要求,确保到2020年我国现行标准下农村贫困人口实现脱贫,贫困县全部摘帽,解决区域性整体贫困,做到脱真贫、真脱贫.某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记x表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“x不超过3”的概率;
(2)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专项规定.某小区采取一系列措施,宣传垃圾分类的知识与意义,并采购分类垃圾箱.为了了解垃圾分类的效果,该小区物业随机抽取了200位居民进行问卷调查,每位居民对小区采取的措施给出“满意”或“不满意”的评价.根据调查结果统计并做出年龄分布条形图和持不满意态度的居民的结构比例图,如图,在这200份问卷中,持满意态度的频率是0.65.
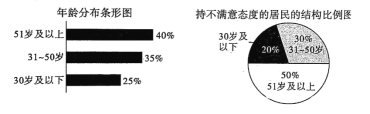
(1)完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
满意 | 不满意 | 总计 | |
51岁及以上的居民 | |||
50岁及以下的居民 | |||
总计 | 200 |
(2)按“51岁及以上”和“50岁及以下”的年龄段采取分层抽样的方法从中随机抽取5份,再从这5份调查问卷中随机抽取2份进行电话家访,求电话家访的两位居民恰好一位年龄在51岁及以上,另一位年龄在50岁及以下的概率.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附表及参考公式: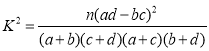 ,其中
,其中![]() .
.